Biomedical Optics: Principles, Imaging Technologies, and Applications in Research and Drug Development

Abstract

This article provides a comprehensive overview of the fundamental principles and cutting-edge applications of biomedical optics, tailored for researchers, scientists, and drug development professionals. It explores how light interacts with biological tissues through absorption, scattering, and fluorescence, and details key technologies like Optical Coherence Tomography (OCT), Photoacoustic Tomography (PAT), and near-infrared spectroscopy. The scope extends from foundational concepts and methodological applications to practical troubleshooting in optical device development and a comparative analysis with other imaging modalities. The content aims to serve as a critical resource for leveraging optical imaging in drug discovery, diagnostic applications, and preclinical research.

Light and Tissue: Core Principles of Light-Tissue Interaction

Biomedical optics is a cornerstone of modern life sciences, providing non-invasive tools for research, diagnostics, and therapy. This field leverages the fundamental interactions between light and biological matter—primarily absorption, scattering, and fluorescence—to investigate and influence processes at molecular, cellular, tissue, and organ levels [1]. These light-based techniques offer significant advantages including non-contact measurement, high sensitivity down to single molecules, rapid real-time data acquisition, and the ability to observe dynamic biological processes across various timescales [1]. This whitepaper details the core principles, measurement methodologies, and research applications of these fundamental interactions, providing a technical foundation for researchers and drug development professionals advancing optical technologies in medicine.

Core Principles of Light-Tissue Interactions

Photons interacting with biological tissue undergo several key processes that form the basis for most biophotonic techniques. The structural, functional, mechanical, biological, and chemical properties of biological materials are studied through these light interactions [1].

Absorption

Absorption occurs when photon energy is transferred to a molecule, promoting it to an excited electronic state. The absorbing molecule converts this photon energy into electrical, vibrational, or thermal energy [2]. This process is quantified by the absorption coefficient µa, which indicates the probability of absorption per unit path length.

• Energy Conversion: The absorbed energy may be re-emitted through mechanisms like fluorescence, converted to heat through photothermal processes, or drive photochemical reactions [2].
• Molecular Specificity: Absorption is highly molecule-specific, with endogenous chromophores including hemoglobin, NADP(H), flavin, elastin, and cytochrome exhibiting characteristic absorption spectra [1].

Scattering

Scattering changes the trajectory of light photons upon interaction with microscopic variations in tissue refractive index. Unlike absorption, scattering typically involves no energy loss. The primary forms are elastic (Rayleigh and Mie) and inelastic (Raman) scattering.

• Elastic Scattering: Photons change direction without wavelength change. This phenomenon underpins techniques like Optical Coherence Tomography (OCT), which detects changes in refractive index to visualize tissue architecture [1].
• Inelastic Scattering: Photons change direction and undergo energy/wavelength shifts, providing molecular vibration information. Raman scattering is molecule-specific, visualizing distributions of proteins, lipids, and DNA, though its weak signal often requires enhancement techniques like coherent Raman scattering (CRS) [1].

Fluorescence

Fluorescence is the emission of longer-wavelength light following photon absorption. Molecules (fluorophores) absorb specific wavelength light, enter an excited state, and emit light upon returning to ground state.

• Endogenous vs. Exogenous: Fluorescence can originate from native fluorophores (e.g., NADP(H), flavins) or introduced labels. Fluorescence imaging and Fluorescence Lifetime Imaging (FLIM) provide spatial distribution and microenvironment information [1].
• Contrast Mechanism: This emission provides high molecular contrast, enabling visualization of specific molecular markers and cellular conditions [1].

The following diagram illustrates the fundamental interactions and their connections to established biomedical techniques.

Quantitative Parameters and Measurement

Quantifying light-tissue interactions requires precise measurement of specific parameters that characterize each interaction type. The following table summarizes the key quantitative metrics, their definitions, and representative values in biological tissues.

Table 1: Key Quantitative Parameters for Light-Tissue Interactions

Parameter	Symbol	Definition	Typical Range in Tissue	Primary Measurement Technique
Absorption Coefficient	µa	Probability of photon absorption per unit path length (mm⁻¹).	0.01 - 10 mm⁻¹ (varies strongly with wavelength and chromophore)	Photoacoustic Imaging (PAI), Diffuse Reflectance Spectroscopy (DRS) [1]
Reduced Scattering Coefficient	µs'	Probability of photon scattering per unit path length, adjusted for anisotropy (mm⁻¹).	1 - 20 mm⁻¹ (NIR region)	Optical Coherence Tomography (OCT), Diffuse Reflectance Spectroscopy (DRS) [1]
Fluorescence Quantum Yield	QY	Ratio of photons emitted to photons absorbed.	0.01 - 0.9 (depends on fluorophore and environment)	Fluorescence Imaging, Fluorescence Lifetime Imaging (FLIM) [1]
Fluorescence Lifetime	Ï„	Average time a fluorophore remains in the excited state before emission (nanoseconds).	1 - 10 nanoseconds	Fluorescence Lifetime Imaging (FLIM) [1]
Thermal Diffusion Length	µ	Distance heat propagates in a material during the laser pulse or modulation period (μm).	Function of modulation frequency and tissue thermal properties [3]	Photoacoustic Sensing [3]

The thermal diffusion length (µ) is a critical parameter in techniques like photoacoustic sensing, where it is calculated as μ = √(k / (π * ρ * f * c)), where k is thermal conductivity, ρ is density, c is specific heat, and f is the modulation frequency of the light [3].

Experimental Methodologies and Protocols

This section provides detailed protocols for investigating the fundamental interactions using common biophotonic techniques.

Protocol: Photoacoustic Imaging (PAI) for Absorption Mapping

Photoacoustic Imaging leverages light absorption to generate acoustic waves for deep-tissue imaging. The following workflow details the experimental setup and procedure.

1. Objective: To map the distribution of optical absorbers (e.g., hemoglobin, melanin) in biological samples by detecting ultrasonic waves generated by light absorption.

2. Materials and Equipment:

• Pulsed Laser Source: Nd:YAG laser or Ti:Sapphire laser with nanosecond pulse duration, tunable in the visible to NIR range (e.g., 532-1064 nm) [3].
• Ultrasound Transducer: Focused single-element transducer or array transducer with central frequency matched to desired resolution/depth (e.g., 10-50 MHz) [3].
• Data Acquisition System: High-speed digitizer for recording photoacoustic signals.
• 3D Motorized Stage: For raster-scanning the transducer or sample.
• Acoustic Coupling Medium: Ultrasound gel or water for signal transmission.

3. Procedure: 1. Sample Preparation: Place the biological sample (e.g., tissue section, small animal) in the imaging chamber. Ensure proper acoustic coupling between the sample and transducer. 2. System Alignment: Align the laser beam to co-axially overlap with the ultrasound transducer focus. For OR-PAM, focus the laser beam using an objective lens [3]. 3. Data Acquisition: * Set the laser wavelength to target specific chromophores. * Initiate raster scanning over the region of interest. * At each point, the laser fires a pulse. The resulting photoacoustic signal is detected by the transducer, converted to an electrical signal, and recorded by the data acquisition system [3]. 4. Signal Processing: * Apply band-pass filtering to the raw signals to reduce noise. * For each scan point, the amplitude of the detected photoacoustic signal is proportional to the local absorption coefficient [3]. 5. Image Reconstruction: Use a reconstruction algorithm (e.g., back-projection) to convert the time-resolved acoustic signals from all scan points into a 2D or 3D map of optical absorption.

Protocol: Spatial Frequency Domain Imaging (SFDI) for Absorption and Scattering Quantification

1. Objective: To quantitatively map the optical absorption (µa) and reduced scattering (µs') coefficients over a wide field of view by analyzing the demodulation of structured illumination patterns.

2. Materials and Equipment:

• Projection System: Digital Light Projector (DLP) or LCD projector.
• Scientific Camera: CCD or CMOS camera with appropriate lens.
• Light Source: Broadband (e.g., halogen) or multiple laser diodes/LEDs.
• Computer: For pattern generation, control, and data analysis.

3. Procedure: 1. Pattern Projection: Project sinusoidal illumination patterns of known spatial frequencies (e.g., 0 mm⁻¹ and 0.2 mm⁻¹) onto the sample surface at multiple phases (typically 0°, 120°, 240°). 2. Image Acquisition: For each pattern frequency and phase, capture a reflected image with the camera. 3. Demodulation: At each pixel, process the three phase-shifted images to compute a demodulated reflectance image, which separates the contribution of the projected pattern from the ambient light. 4. Model Fitting: Use a light transport model (e.g., diffusion approximation or Monte Carlo simulation) to fit the measured reflectance at multiple spatial frequencies, thereby extracting pixel-wise maps of µa and µs'.

The Scientist's Toolkit: Essential Research Reagents and Materials

Successful experimentation in biomedical optics requires specific reagents and materials. The following table details key solutions for the featured photoacoustic imaging experiment and the broader field.

Table 2: Research Reagent Solutions for Biophotonics Experiments

Item Name	Function/Application	Specific Example/Note
Phosphate Buffered Saline (PBS)	Washing and suspending cells (e.g., Red Blood Cells - RBCs) to maintain osmotic balance and physiological pH during preparation for PAI [3].	Isotonic PBS is used to wash RBCs two times after centrifugation to separate plasma [3].
Acoustic Coupling Gel	Ensures efficient transmission of generated acoustic waves from the sample to the ultrasound transducer in contact PAI modes [3].	Standard ultrasound gel; water can also be used as a coupling medium in non-contact configurations [3].
Exogenous Contrast Agents	Enhances optical absorption at specific wavelengths to improve signal-to-noise ratio for targeting molecular biomarkers.	Includes organic dyes (e.g., ICG), gold nanoparticles, and carbon nanotubes.
Objective Lens	Focuses the excitation laser beam to a small spot size for high-resolution Optical-Resolution PAM (OR-PAM) [3].	Infinity-corrected objectives (e.g., 40x, 0.25 NA) are used to focus the laser onto the sample [3].
Resonator Column	Amplifies weak, continuous-wave laser-induced photoacoustic signals to detectable levels in specific sensor designs [3].	The design of the resonator column and sample chamber size critically affects the quality factor and signal amplification [3].
Egfr-TK-IN-4	Egfr-TK-IN-4, MF:C23H16F2N6O2S2, MW:510.5 g/mol	Chemical Reagent
Tegacorat	Tegacorat, CAS:2409551-99-9, MF:C22H20F3N5O2S, MW:475.5 g/mol	Chemical Reagent

Advanced Techniques and Applications

Non-linear optical phenomena have significantly advanced biomedical imaging, enabling greater penetration depth and spatial resolution.

Multi-Photon and Harmonic Generation Microscopy

Multi-photon absorption occurs when a fluorophore simultaneously absorbs two or more longer-wavelength (typically NIR) photons. The combined energy excites the molecule, followed by fluorescence emission.

• Advantages: The use of NIR femtosecond lasers reduces scattering and allows deeper tissue imaging. The excitation is confined to a tiny focal volume, providing inherent optical sectioning and reduced photobleaching outside the focal plane [1].
• Harmonic Generation: Second Harmonic Generation (SHG) and Third Harmonic Generation (THG) are non-linear scattering processes where two or three photons combine to generate a new photon at exactly half or one-third the wavelength, respectively. SHG is particularly useful for visualizing non-centrosymmetric structures like collagen [1].

Coherent Raman Scattering (CRS) Microscopy

Techniques like Coherent Anti-Stokes Raman Scattering (CARS) and Stimulated Raman Scattering (SRS) overcome the inherent weakness of spontaneous Raman scattering.

• Principle: These methods use multiple laser beams to coherently drive molecular vibrations, resulting in a signal enhancement of several orders of magnitude compared to linear Raman scattering [1].
• Application: CRS enables high-speed, label-free chemical imaging of biomolecules such as lipids and proteins within living cells and tissues, bypassing the need for fluorescent labels [1].

The fundamental interactions of light—absorption, scattering, and fluorescence—provide the underlying framework for a powerful and expanding suite of tools in biomedical research. The quantitative parameters and detailed experimental protocols outlined in this whitepaper serve as a foundation for researchers developing new diagnostic methods, therapeutic interventions, and drug development platforms. As biophotonics continues to evolve, driven by advancements in lasers, detectors, and artificial intelligence, these core principles will remain essential for unlocking deeper insights into biological processes and disease mechanisms, ultimately paving the way for next-generation precision medicine.

The quantitative measurement of tissue optical properties is a cornerstone of biomedical optics, essential for both therapeutic and diagnostic applications [4]. The manner in which light propagates within and interacts with biological tissues provides critical information on tissue architecture and physiology, which can directly quantify damage or abnormalities [5]. This interaction is primarily governed by two fundamental optical properties: the absorption coefficient (μa) and the reduced scattering coefficient (μs'). These intrinsic parameters determine the measurable transmission and reflection of light, and their accurate estimation is vital for technologies ranging from photodynamic therapy and photocoagulation to non-invasive disease diagnosis and health monitoring [6] [4].

The field has evolved from simple qualitative assessments to sophisticated quantitative methods that leverage computational modeling. The ability to disentangle the effects of absorption and scattering from measured light signals allows researchers to extract meaningful physiological data, such as blood oxygen saturation and tissue composition [7]. This guide provides an in-depth technical examination of these core optical properties, their measurement methodologies, and their significance within biomedical research.

Defining the Fundamental Optical Properties

When light is incident on biological tissue, a portion is reflected at the air-tissue interface due to refractive index mismatch. The remaining light penetrates the tissue and undergoes a series of absorption and scattering events, which spatially broaden and attenuate the light before some of it escapes as diffuse reflectance or transmittance [6]. The following parameters are used to quantitatively describe these processes.

Absorption Coefficient (μa)

The absorption coefficient (μa) is defined as the probability of a photon being absorbed per unit pathlength of travel through the medium, with a typical order of magnitude of 0.1 cm⁻¹ in the near-infrared (NIR-I) window [6]. Absorption occurs in tissue chromophores—the light-absorbing molecules within tissue. The total μa is a linear combination of the molar extinction coefficients (ε) for all chromophores present, weighted by their concentrations (C) [6] [8]. This relationship is described by: μa = ln(10) Σ (εi Ci) [8].

The dominant chromophores in blood are oxyhemoglobin (HbOâ‚‚) and deoxyhemoglobin (HHb), whose distinct absorption spectra in the visible and NIR wavelengths enable the determination of oxygen saturation [6]. Other significant chromophores include water, lipids, melanin, and collagen [6]. The ratio of oxyhemoglobin concentration to total hemoglobin concentration defines the oxygen saturation (StOâ‚‚), a key biomarker in clinical applications such as tissue oxygenation monitoring [6] [9].

Scattering Properties

Scattering in tissue arises from refractive index inhomogeneities, such as variations between subcellular organelles (e.g., nuclei, mitochondria) and their surrounding cytoplasmic medium [6].

• Scattering Coefficient (μs): The scattering coefficient (μs) is defined as the probability of photon scattering per unit pathlength, with a typical order of magnitude of 100 cm⁻¹ in the NIR-I window. The inverse of μs is the scattering mean free path (mfpâ‚›), which represents the average distance a photon travels between two scattering events [6].
• Anisotropy Factor (g): Scattering in biological tissues is not isotropic but strongly forward-directed. The anisotropy factor (g) is defined as the average cosine of the scattering angle (θ), with values ranging from 0 (perfectly isotropic scattering) to 1 (purely forward scattering). Most biological tissues have a g value of approximately 0.9 [6].
• Reduced Scattering Coefficient (μs'): Given the highly forward-directed nature of scattering, the reduced scattering coefficient (μs') is defined as μs' = μs(1 - g). This parameter represents the probability of equivalent isotropic photon scattering per unit pathlength in the diffusive regime and has a typical order of magnitude of 10 cm⁻¹ in the NIR-I window [6] [9]. The mean free path between effectively isotropic scattering events (mfpâ‚›') is 1/μs'.

Derived Parameters in Diffusion Theory

When light propagation becomes diffusive after multiple scattering events, several parameters are derived from μa and μs' to characterize the light field, as summarized in Table 1.

Table 1: Key Parameters for Characterizing Tissue Optical Properties

Parameter	Symbol	Definition	Common Unit
Absorption Coefficient	μa	Probability of photon absorption per unit pathlength	cm⁻¹ or mm⁻¹
Scattering Coefficient	μs	Probability of photon scattering per unit pathlength	cm⁻¹ or mm⁻¹
Anisotropy Factor	g	Average cosine of the scattering angle,	Unitless
Reduced Scattering Coefficient	μs'	μs' = μs(1 - g)	cm⁻¹ or mm⁻¹
Transport Coefficient	μt'	μt' = μa + μs'	cm⁻¹ or mm⁻¹
Diffusion Coefficient	D	D = [3(μa + μs')]⁻¹	mm or cm
Effective Attenuation Coefficient	μeff	μeff = √(μa / D) = √[3μa(μa + μs')]	cm⁻¹ or mm⁻¹

Measurement Techniques and Experimental Protocols

A range of techniques has been developed to measure the optical properties of biological tissues. These methods can be broadly categorized as steady-state (or continuous wave), time-domain, frequency-domain, spatial-domain, and spatial frequency-domain imaging [6]. The experimental measurements are coupled with computational models of light-tissue interactions to inversely solve for μa and μs' from the measured reflectance and/or transmittance [6].

Integrating Sphere Technique

The integrating sphere (IS) is a standard apparatus for measuring total diffuse reflectance and total transmittance, which serve as inputs for inverse models to determine μa and μs' [10] [5].

• Protocol Overview: A thin slice of tissue is illuminated by a collimated beam, and both the diffusely reflected and transmitted light are collected and integrated by the sphere(s) [4]. The inner surface of the sphere is coated with a high-reflectivity material (reflectance > 98%) to uniformly distribute the captured light, which is then detected by a spectrometer [10].
• System Configurations:
  • Single Integrating Sphere (SIS): Allows for stepwise measurement of diffuse reflectance and transmittance by alternately positioning the sample at the reflectance or transmittance port. Four ports are typically located at the equatorial plane (0°, 90°, 180°) and the top of the sphere. The 0° port is connected to a light source, while detectors are placed at other ports [10].
  • Double Integrating Sphere (DIS): A sample is sandwiched between two spheres, enabling simultaneous measurement of diffuse reflectance (Rd) and transmittance (Td). This configuration, coupled with collimated transmittance (Tc) measurement, provides a more complete data set for inverse analysis, improving the accuracy of extracted optical properties [10].
• Inverse Models: The measured Rd and Td are fed into an inverse model to calculate μa and μs'. Common models include:
  • Inverse Adding-Doubling (IAD): An iterative technique where a set of optical properties is guessed, and the corresponding reflection and transmission are calculated using the adding-doubling method. The process repeats until the calculated values match the measured values [10] [11].
  • Inverse Monte Carlo (IMC): Uses stochastic simulations of photon propagation to find the optical properties that best reproduce the measured data [10].
  • Kubelka-Munk (KM) Model: A simpler, two-flux model that directly relates Rd and Td to the absorption (K) and scattering (S) coefficients. Its parameters are frequently used in medical physics due to its relative simplicity [5].

The workflow for the double integrating sphere method is illustrated below.

Spatially Resolved (SR) and Time-Domain (TD) Techniques

Other prominent methods focus on measuring the spatial or temporal distribution of light.

• Spatially Resolved (SR): This method acquires the radially dependent diffuse reflectance profile, R(ρ), versus the source-detector distance (ρ). The resulting data is then inverted to estimate μa and μs' [10] [9]. In continuous-wave (CW) systems, this approach is the basis for commercial near-infrared spectroscopy (NIRS) devices that estimate tissue oxygen saturation [9].
• Time-Domain (TD): This technique records the temporal point-spread function, I(t), of diffusely propagating photons following ultrashort pulse illumination. By fitting the temporal distribution of detected light with a model based on diffusion theory or Monte Carlo simulations, μa and μs' can be estimated [10] [9]. This method provides rich data but requires relatively complex instrumentation [10].
• Time-Domain Spatially Resolved (TD-SRS): A hybrid approach extends the SRS methodology to the time domain. It calculates the spatial derivative of the time-dependent attenuation, A(ρ,t), to estimate μs' [9]. This method can assess the spatial homogeneity of scattering in the explored tissue [9].

The logical relationship between the primary measurement methods is summarized in the following diagram.

Quantitative Data of Tissue Optical Properties

The optical properties of tissues vary significantly across tissue types and wavelengths. Table 2 provides representative values for key biological materials in the red and near-infrared (NIR) spectral range, which is often called the "therapeutic window" due to reduced absorption by hemoglobin and water, allowing for deeper light penetration.

Table 2: Representative Optical Properties of Biological Tissues at Near-Infrared Wavelengths

Tissue / Material	Absorption Coefficient μa (cm⁻¹)	Reduced Scattering Coefficient μs' (cm⁻¹)	Anisotropy Factor (g)	Notes	Source
Whole Blood	Varies with Hb content	~13	~0.99	Highly dependent on hematocrit, oxygenation; scattering is strongly forward-directed.	[8]
Skin	~0.1	~10 - 20	~0.9	Properties vary with hydration; dry skin shows different scattering.	[6] [5]
Adipose Fat	Low (dominated by lipids)	Moderate	~0.9	Optical parameters change with boiling (structural alteration).	[5]
General Tissue (NIR)	~0.1	~10	~0.9	Typical orders of magnitude in the NIR-I window (650-950 nm).	[6]

The Scientist's Toolkit: Essential Research Reagents and Materials

Successful experimentation in tissue optics requires specific instruments, computational tools, and sample preparation materials. Table 3 details key components of a typical research toolkit.

Table 3: Essential Research Reagent Solutions and Materials

Item	Function / Explanation
Integrating Sphere	A core instrument for measuring total diffuse reflectance and transmittance from tissue samples. The inner wall is coated with a highly reflective material (e.g., Spectralon) to integrate light uniformly. [10] [5]
Tissue-Mimicking Phantoms	Reference standards with known and stable optical properties, used for system calibration and validation. Often made from materials like polyurethane or liquid suspensions with calibrated scatterers (e.g., TiOâ‚‚, polystyrene microspheres) and absorbers (e.g., India ink, nigrosin). [10]
Inverse Adding-Doubling (IAD) Software	A standard computational algorithm for extracting the absorption and reduced scattering coefficients (μa, μs') from integrating sphere measurements (Rd, Td). [10] [11]
Monte Carlo Simulation Package	A computational method for modeling the random walk of photons in a scattering medium. It is used as a forward model to predict light transport or as an inverse model (IMC) to extract optical properties. [10] [12]
High-Sensitivity Spectrometer	For resolving spectral measurements of diffuse reflectance and transmittance, enabling the decomposition of μa into contributions from individual chromophores.
Thin Sample Holder	For preparing and mounting tissue samples of precise, uniform thickness (e.g., 2-3 mm), which is critical for accurate transmission and reflection measurements. [5]
Friluglanstat	Friluglanstat, CAS:1422203-86-8, MF:C25H20ClF3N4O3, MW:516.9 g/mol
3,4-DAA	3,4-DAA, MF:C18H17NO6, MW:343.3 g/mol

The absorption coefficient μa and the reduced scattering coefficient μs' are fundamental parameters that quantitatively describe light transport in biological tissues. As detailed in this guide, a suite of well-established techniques, notably integrating sphere measurements coupled with inverse models like IAD, enables their accurate determination. These optical properties are not merely abstract numbers; they provide a window into tissue composition, microstructure, and physiological status.

The field continues to advance with the integration of artificial intelligence and machine learning, which enhances the accuracy of inverse models and the robustness of optical property estimation [10]. Furthermore, the development of portable and cost-effective systems is promoting the translation of these techniques from research labs to clinical and point-of-care settings [10] [7]. A deep understanding of these core optical properties and their measurement is, therefore, indispensable for any researcher or professional working in biomedical optics, drug development, and diagnostic technology innovation.

Biomedical optical imaging technologies provide non-invasive methods for diagnosing and monitoring diseases by leveraging the unique ways light interacts with biological tissues. These interactions, which include absorption, scattering, and fluorescence, generate contrast that reveals both structural and functional information about tissue health and composition. The most significant endogenous chromophores—hemoglobin, lipids, and water—each possess distinct absorption profiles across the optical spectrum. Their concentrations and spatial distribution within tissue serve as key indicators of physiological status, signaling conditions such as tumor formation, inflammation, and metabolic disorders. This technical guide details the molecular origins of optical contrast, quantitative concentration ranges found in biological tissues, experimental protocols for measurement, and the advanced imaging technologies that exploit these properties for research and clinical applications. A comprehensive understanding of these principles is fundamental to advancing biomedical optics research and developing new diagnostic and therapeutic strategies.

Table 1: Core Endogenous Chromophores and Their Roles in Optical Contrast.

Chromophore	Primary Optical Significance	Key Absorption Peaks (nm)	Physiological Correlation
Hemoglobin (Oxy)	Dominant absorber in NIR window; oxygen delivery	~540, ~580, ~850 [13]	Blood volume, tissue oxygenation, metabolism
Hemoglobin (Deoxy)	Dominant absorber in NIR window; oxygen consumption	~560, ~760 [14]	Oxygen consumption, hypoxic states
Lipids	Major absorber in SWIR; structural and energy storage	~930, ~1210 [15]	Adipose tissue content, metabolic disease, certain tumors
Water	Dominant absorber in SWIR; tissue hydration	~980, ~1200 [15]	Tissue edema, cystic structures

Quantitative Chromophore Properties and Tissue Concentrations

Accurate quantification of chromophore concentrations is vital for interpreting optical imaging data. The absorption coefficient of tissue (μₐ) is a linear combination of the concentration of each constituent chromophore multiplied by its specific wavelength-dependent absorption coefficient. This relationship is formalized as μₐ(λ) = Σ cᵢ ∙ εᵢ(λ), where cᵢ is the concentration and εᵢ(λ) is the molar absorption spectrum of the i-th chromophore. The reduced scattering coefficient (μₛ'), which describes how light is scattered in tissue, is often modeled using an approximation to Mie scattering theory: μₛ'(λ) = A ∙ λ^(-SP), where A is a scaling amplitude and SP is the scattering power related to the size and density of scattering particles [16].

The following tables summarize typical concentration ranges for key chromophores in healthy and pathological tissues, providing a critical reference for data interpretation.

Table 2: Typical Chromophore Concentration Ranges in Human Breast Tissue [16].

Tissue Component	Concentration Range	Notes and Correlations
Total Hemoglobin (HbT)	10 - 60 μM	Inversely correlated with body mass index (BMI).
Hemoglobin Oxygen Saturation (StOâ‚‚)	0 - 90%	Varies with tissue type and metabolic activity.
Water Fraction	11 - 74%	Higher in glandular tissue, lower in adipose tissue.
Lipid Fraction	26 - 90%	Higher in adipose tissue; average breast is ~81% adipose.

Table 3: Optical Property Ranges for Biological Tissues (600-1000 nm).

Optical Property	Typical Range in Tissue	Governed By
Absorption Coefficient (μₐ)	0.001 - 0.05 mm⁻¹	Chromophore concentration and type (Hb, H₂O, lipids) [14]
Reduced Scattering Coefficient (μₛ')	0.5 - 2.0 mm⁻¹	Density and size of cellular and subcellular structures [16]
Scattering Power (SP)	Varies with tissue structure	Higher in fibrous/glandular tissue, lower in fatty tissue [16]

Experimental Methodologies for Contrast Measurement

Diffuse Reflectance Spectroscopy for Hemoglobin and Water

Objective: To non-invasively quantify concentrations of oxyhemoglobin (HbOâ‚‚), deoxyhemoglobin (HbR), and water (Hâ‚‚O) in tissue using diffuse optical spectroscopic imaging (DOSI).

Protocol:

• System Setup: Utilize a DOSI system combining frequency-domain and continuous-wave components. The frequency-domain component typically uses laser diodes at multiple wavelengths (e.g., 660-850 nm) modulated at high frequencies (50-600 MHz). The continuous-wave component employs a broadband white light source and a spectrometer to sample a wide spectrum (e.g., 580-1020 nm) [17] [16].
• Data Acquisition: Place the optical probe in gentle contact with the tissue surface. Acquire frequency-domain data to determine the absolute absorption (μₐ) and reduced scattering (μₛ') coefficients at discrete wavelengths. Use these as a baseline to calibrate the hyperspectral continuous-wave data, converting measured diffuse reflectance into accurate μₐ(λ) spectra across all wavelengths [17].
• Spectral Fitting: Perform a linear least-squares fit of the measured absorption spectrum using the known molar absorption spectra of the target chromophores (HbOâ‚‚, HbR, Hâ‚‚O). The fitting model is μₐ(λ) = [εHbOâ‚‚(λ)]·[HbOâ‚‚] + [εHbR(λ)]·[HbR] + [ε_Hâ‚‚O(λ)]·[Hâ‚‚O]. Positivity constraints are applied to ensure non-negative concentrations [14] [16].
• Calculation of Derived Parameters:
  • Total Hemoglobin: HbT = [HbOâ‚‚] + [HbR]
  • Oxygen Saturation: StOâ‚‚ = [HbOâ‚‚] / HbT × 100%

Shortwave Infrared Meso-Patterned Imaging (SWIR-MPI) for Water and Lipids

Objective: To provide non-contact, label-free spatial mapping of water and lipid concentrations in tissue by exploiting their strong absorption in the shortwave infrared (SWIR) region.

Protocol:

• System Setup: Employ a SWIR-MPI system with a wavelength-tunable pulsed laser (680-1300 nm) and a digital micromirror device (DMD) to project structured illumination patterns (e.g., DC and AC spatial frequencies) onto the tissue. Remitted light is captured by a SWIR-sensitive germanium CMOS camera [15].
• Data Acquisition: Acquire images of the sample under patterned illumination at multiple wavelengths across the SWIR range (900-1300 nm), specifically targeting the absorption peaks of water (~980, ~1200 nm) and lipids (~930, ~1210 nm).
• Inverse Model and Lookup Table (LUT): Demodulate the acquired images to obtain diffuse reflectance at different spatial frequencies for each pixel. Input these values into an inverse model that references a pre-computed LUT generated from Monte Carlo simulations of light transport. The LUT maps the measured reflectance patterns to unique combinations of μₐ and μₛ' [15].
• Chromophore Concentration Mapping: Apply Beer's law to the extracted μₐ spectra on a pixel-by-pixel basis. Fit the spectra using the known extinction coefficients of water and lipids to generate spatial concentration maps. Concentrations are reported as percentages relative to pure water (55.6 M) and pure lipid (0.9 g/ml) [15].

Optimal Wavelength Selection Algorithm

Objective: To systematically select an optimal set of wavelengths for accurate spectral fitting of diffuse reflectance data, improving the stability and precision of chromophore concentration estimates.

Protocol:

• Construct Basis Matrix: Create a wavelength-dependent pathlength-modulated absorption matrix (μaL) for an oversampled set of wavelengths. Each row represents a wavelength, and each column represents a pathlength-modulated absorption spectrum for a specific chromophore (e.g., HbOâ‚‚, HbR, Hâ‚‚O) [14].
• Iterative Wavelength Removal:
  • Start with the full oversampled matrix.
  • For each row (wavelength), compute a selection metric after its temporary removal.
• Selection Criterion: The optimal metric is the product of all singular values of the matrix (a measure of its overall orthogonality and stability). Maximizing this product, rather than just optimizing the condition number or the smallest singular value, has been shown to yield lower RMS errors in concentration estimates [14].
• Elimination and Iteration: Permanently remove the wavelength whose elimination results in the largest product of singular values. Repeat the process until the desired number of wavelengths is achieved. This algorithm typically identifies robust wavelength combinations, such as 532 nm, 596 nm, and 616 nm for fitting HbOâ‚‚, HbR, and Hâ‚‚O [14].

Diagram 1: Workflow for optimal wavelength selection via singular value maximization.

Visualization of Contrast Origins and Workflows

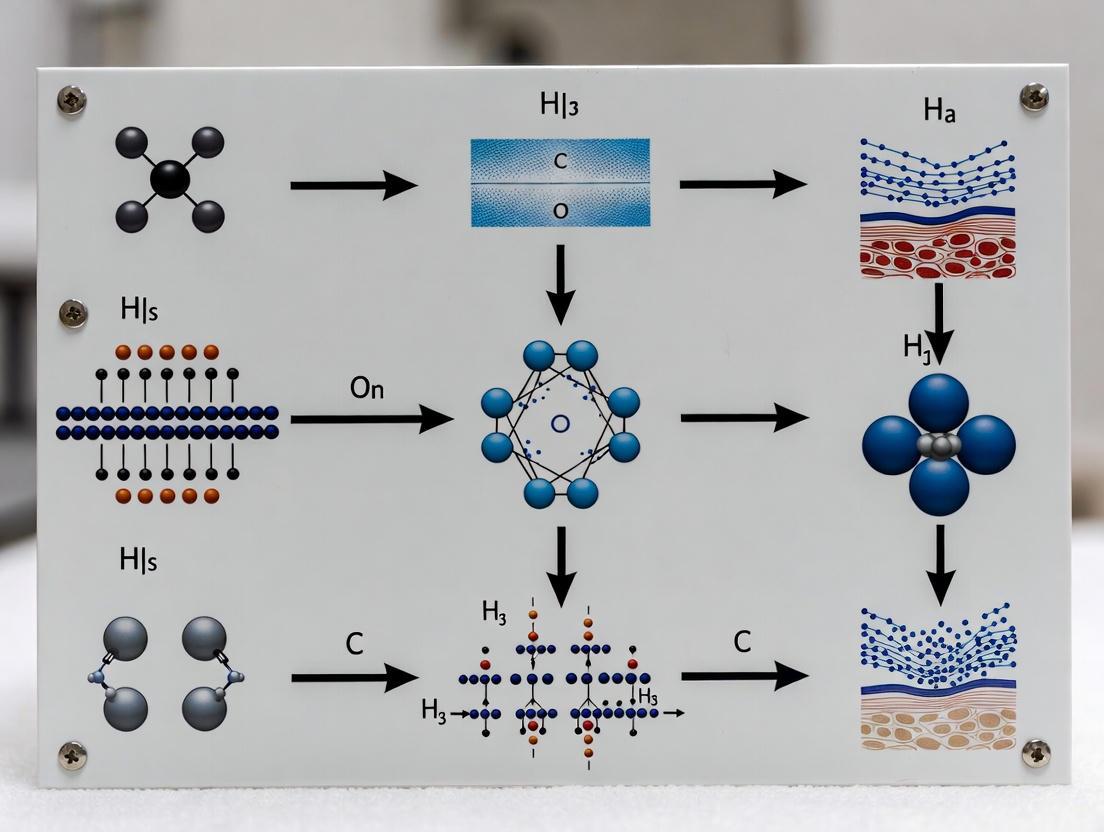
The diagnostic power of optical imaging stems from the direct relationship between tissue molecular composition and the resulting optical signals. The following diagram illustrates the causal pathway from a tissue's underlying biology to the measurable contrasts used in various imaging modalities.

Diagram 2: The signal pathway from molecular composition to optical contrast.

The Scientist's Toolkit: Research Reagents and Materials

Successful experimentation in biomedical optics relies on a suite of specialized materials and reagents for system calibration, phantom validation, and contrast enhancement.

Table 4: Essential Research Reagents and Materials for Optical Spectroscopy and Imaging.

Category / Item	Specific Examples	Function and Application	Key Characteristics
Tissue-Simulating Phantoms	Intralipid emulsion [16], Solid resin phantoms [17]	System validation, calibration, and performance testing.	Tissue-like μₐ and μₛ'; highly repeatable; durable.
Anthropomorphic Phantoms	Lard-guar gum matrices [17], Hemoglobin-doped phantoms [17]	Mimicking realistic tissue geometry and composition.	Physiological water:lipid ratios; incorporates Hb; free-standing.
Emulsifying Agents	Guar gum, Soy lecithin, Borax [17]	Creating stable, semi-solid phantoms with high lipid content.	Ubiquitous, inexpensive, non-toxic; provides structural scaffolding.
Blood & Hemoglobin Sources	Porcine blood [17], Whole human blood [16]	Simulating vascularization and oxygen metabolism in phantoms.	Provides native HbOâ‚‚ and HbR; enables StOâ‚‚ studies.
Scattering Agents	Intralipid [16], Titanium dioxide (TiO₂) [17]	Adjusting the reduced scattering coefficient (μₛ') of phantoms.	Controlled particle size; predictable scattering spectra.
Exogenous Contrast Agents	Indocyanine Green (ICG) [18] [19], Targeted nanoparticles [19]	Enhancing contrast for specific molecular targets (e.g., tumors).	High absorption in optical window; biocompatible.
Btk-IN-15	Btk-IN-15, MF:C28H24FN5O2, MW:481.5 g/mol	Chemical Reagent	Bench Chemicals
STING antagonist 1	STING antagonist 1, MF:C31H30FN7, MW:519.6 g/mol	Chemical Reagent	Bench Chemicals

Theoretical Foundations of Light Propagation in Tissue

The Radiative Transport Equation (RTE) is widely considered the most accurate deterministic model for describing light propagation in scattering and absorbing media like biological tissue. It serves as the fundamental equation for investigating particle transport across various scientific fields, including astrophysics, neutron transport, climate research, and biomedical optics [20]. In the context of medical optics, the RTE provides a valid approximation of Maxwell's equations while avoiding the prohibitive computational costs associated with solving them numerically, making it suitable for applications ranging from microscopic volumes to entire organs [20]. The steady-state form of the RTE is expressed as:

Ω · ∇I(x,Ω) + μ_t(x)I(x,Ω) = μ_s(x)∫_S² f(x,Ω,Ω')I(x,Ω')dΩ' + S(x,Ω)

Where:

• I(x,Ω) is the radiance at position x in direction Ω
• μ_t = μ_a + μ_s is the total attenuation coefficient
• μ_a and μ_s are the absorption and scattering coefficients, respectively
• f(x,Ω,Ω') is the scattering phase function
• S(x,Ω) is the internal source distribution [20]

The RTE is an integro-differential equation that balances gains and losses of photons traveling through a medium. The terms represent, in order: the net change of radiance in a specific direction, losses due to absorption and scattering out of the direction, gains from scattering into the direction from all other directions, and contributions from internal light sources.

The scattering phase function f(x,Ω,Ω') describes the probability of light scattering from direction Ω' to Ω. In biomedical optics, the Henyey-Greenstein phase function is commonly used, though simplified approximate MIE (SAM) phase functions have also been developed to better fit Mie theory for tissue applications [21].

For modeling light propagation at boundaries between different media (such as tissue-air interfaces), the RTE must be solved with appropriate boundary conditions. A common approach uses the Fresnel reflection coefficient:

I(y,Ω) = R_f(-Ω · n̂)I(y,Ω̄) for Ω · n̂ < 0

Where R_f(μ) is the Fresnel reflection coefficient, n̂ is the outward normal vector, and Ω̄ = Ω - 2(n̂ · Ω)n̂ is the reflection of vector Ω on the tangent plane [20].

The Diffusion Approximation to the RTE

The Diffusion Approximation (DA) is a widely used simplification of the RTE that offers computational efficiency while maintaining reasonable accuracy for many biomedical applications. The DA is derived by expressing the radiance and phase function as first-order expansions using spherical harmonics (the P1 approximation), which transforms the RTE into a more tractable form [22].

The time-independent diffusion equation is expressed as:

-∇ · [D(r)∇Φ(r)] + μ_a(r)Φ(r) = S(r)

Where:

• Φ(r) is the photon fluence rate
• D(r) = 1/[3(μ_a + μ_s')] is the diffusion coefficient
• μ_s' = μ_s(1-g) is the reduced scattering coefficient
• g is the anisotropy factor [23]

The DA assumes that light propagation is highly scattering-dominated (μs' >> μa) and that the angular distribution of radiance is nearly isotropic. These assumptions make the DA particularly suitable for modeling light propagation in deep tissue regions where photons have undergone many scattering events.

The relationship between the fundamental RTE and its various approximations can be visualized as follows:

Comparative Analysis of RTE and DA

Performance Characteristics and Limitations

The DA provides accurate predictions in scattering-dominated regimes but fails in specific scenarios where its underlying assumptions break down [24]. The RTE offers superior accuracy but at significantly higher computational cost.

Table 1: Comparison of RTE and Diffusion Approximation Characteristics

Characteristic	Radiative Transport Equation (RTE)	Diffusion Approximation (DA)
Fundamental Nature	Integro-differential equation	Parabolic partial differential equation
Computational Cost	High	Low
Accuracy Near Sources/Boundaries	High accuracy	Poor accuracy
Accuracy in Low-Scattering Regimes	High accuracy	Fails
Accuracy in High-Absorption Regimes	High accuracy	Fails
Angular Resolution	Full angular dependence	Limited (cosine + constant)
Common Solution Methods	Monte Carlo, Discrete Ordinates, Spherical Harmonics, Finite Element Method	Analytical solutions, Finite Element Method

Validity Ranges and Application Boundaries

Numerical studies have established specific validity criteria for the diffusion approximation. Research comparing DA with Monte Carlo simulations (considered a gold standard for verification) has demonstrated that DA can be accurately applied when μs' >> μa, even with sensors located very close to sources (>1mm) [25]. However, the accuracy of DA diminishes significantly when the reduced scattering to absorption ratio decreases below a critical threshold.

Table 2: Validity Ranges of Diffusion Approximation Based on Scattering Properties

Scattering Condition	μs'/μa Ratio	DA Validity	Primary Limitations
High Scattering	>10-30	Reliable in deep tissue	Fails near sources/boundaries
Moderate Scattering	1-10	Limited validity	Inaccurate for small source-detector separations
Low Scattering	<1	Not valid	Cannot predict light distribution
Anisotropic Scattering	Any value with high g	Limited validity	Fails to capture directional effects

The DA is particularly unreliable for predicting angle-resolved radiance because its angular dependence consists only of a cosine plus a constant, which cannot capture the complex angular distributions occurring in tissues [20]. For applications requiring accurate modeling near sources, boundaries, in low-scattering regions, or in tissues with high absorption, the RTE provides substantially better performance.

Advanced Approximation Methods and Hybrid Approaches

Spherical Harmonics (PN) Approximations

PN methods represent a class of approximations between the exact RTE and the simple DA. These methods expand the radiance and phase function in terms of spherical harmonics, with higher values of N providing increased accuracy at the cost of computational complexity. The P1 approximation leads directly to the diffusion equation, while higher-order approximations (P3 and beyond) offer improved accuracy for specific applications [22].

A significant advancement is the δ-PN approximation, which adds a Dirac-δ function to the Legendre polynomial expansion to better model collimated sources and highly forward-scattering media. The δ-P1 approximation, for instance, provides substantially improved predictions for spatially resolved diffuse reflectance at small source-detector separations and for media with moderate or low albedo compared to the standard DA [22].

Hybrid Formulations

Hybrid methods have been developed to leverage the strengths of different modeling approaches while mitigating their weaknesses:

• Coupled RTE-DA Models: These approaches partition the computational domain into regions where the RTE is solved (typically near sources and boundaries) and regions where the DA is sufficient (deep in scattering-dominated tissue) [21]. The solutions are coupled at interfaces through appropriate boundary conditions that ensure conservation of energy and phase continuity.

• Hybrid PN Methods: This approach converts the RTE into an integral equation and incorporates radiance predictions from classical PN methods. The resulting method enables accurate computation of radiance near boundaries of anisotropically scattering media with computational effort similar to traditional PN methods but with significantly improved accuracy [20].

• Neumann-Series RTE: This method formulates the RTE in integral form and expresses the solution as a Neumann series, where successive terms represent successive scattering events. This approach has been extended to incorporate boundary conditions arising from refractive index mismatch, which is crucial for accurate modeling of photon transport in biomedical applications [24].

Experimental Protocols and Implementation

Numerical Solution of RTE Using Discrete Ordinates and Finite Elements

The following protocol outlines a robust method for numerically solving the RTE using the Discrete Ordinate Method (DOM) with a streamline diffusion modified continuous Galerkin finite element method [26]:

Angular Discretization (Discrete Ordinate Method):

• Select an appropriate angular quadrature scheme (e.g., level symmetric, Lebedev, or product Gaussian quadratures) to discretize the angular domain.
• Apply phase function normalization to preserve conservative properties after angular discretization and reduce numerical oscillations.
• Transform the RTE into a system of coupled partial differential equations (PDEs) using the selected quadrature weights and directions.

Spatial Discretization (Streamline Diffusion FEM):

• Discretize the spatial domain using an unstructured mesh capable of representing complex tissue geometries.
• Apply the streamline diffusion modification to the continuous Galerkin method to suppress numerical oscillations caused by the transport nature of the RTE.
• Implement appropriate boundary conditions, including Fresnel reflections at tissue-air interfaces.
• Solve the resulting system of linear equations using iterative methods suitable for large, sparse systems.

Validation:

• Compare computed solutions with Monte Carlo simulations for standardized geometries and optical properties.
• Verify that photon densities match Monte Carlo predictions within approximately 5% in deeper tissue regions with standard optical properties [26].

The workflow for implementing this numerical approach is shown below:

Protocol for δ-P1 Approximation for Spatially Resolved Diffuse Reflectance

This protocol describes how to implement the δ-P1 approximation for predicting spatially resolved diffuse reflectance, which provides more accurate results than the standard DA, particularly at small source-detector separations [22]:

• Medium Characterization:

  • Determine the optical properties of the medium: absorption coefficient (μa), scattering coefficient (μs), and anisotropy factor (g_1).
  • Calculate the modified properties for the δ-P1 approximation:
    • f = g_1²
    • g* = g_1/(1 + g_1)
    • μ_s* = μ_s(1 - f)
    • μ_t* = μ_a + μ_s*

• Solution of the δ-P1 Equations:

  • Implement the analytical solution for the δ-P1 approximation in a semi-infinite geometry with a pencil beam source.
  • Apply the appropriate extrapolated boundary condition for a semi-infinite turbid medium.
  • Compute the spatially resolved diffuse reflectance using the closed-form expressions.

• Inverse Problem for Optical Property Recovery:

  • Develop a multi-stage nonlinear optimization algorithm to recover μa, μs', and g_1 from experimental measurements of spatially resolved diffuse reflectance.
  • Minimize the difference between measured reflectance and predictions from the δ-P1 model.
  • Validate recovered optical properties against known values from phantoms.

This approach has been demonstrated to recover μa, μs', and g1 with errors within ±22%, ±18%, and ±17%, respectively, for both intralipid-based and siloxane-based tissue phantoms across the optical property range 4 < (μs'/μ_a) < 117 [22].

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Essential Computational Methods and Their Applications in Radiative Transport

Method/Technique	Function	Application Context
Monte Carlo Simulation	Stochastic modeling of photon transport	Gold standard for validation; complex geometries
Discrete Ordinate Method (DOM)	Angular discretization of RTE	Numerical solution of RTE in complex domains
Spherical Harmonics (PN)	Angular expansion of radiance	Higher-order approximations to RTE
Finite Element Method (FEM)	Spatial discretization of PDEs	Handling complex tissue geometries and boundaries
δ-PN Approximations	Improved modeling of collimated sources	Media with high anisotropy and small source-detector separations
Neumann-Series RTE	Integral formulation of RTE	Accurate modeling of boundary reflections
Hybrid RTE-DA Models	Coupling of different models	Large domains with both high and low scattering regions
Simplified Approximate MIE (SAM) Phase Function	Approximation of Mie scattering	More accurate scattering models for tissue
HVH-2930	HVH-2930, MF:C29H36N4O3, MW:488.6 g/mol	Chemical Reagent
Nlrp3-IN-29	Nlrp3-IN-29, MF:C21H22N2O3S, MW:382.5 g/mol	Chemical Reagent

These computational tools enable researchers to select appropriate modeling strategies based on their specific application requirements, balancing accuracy, computational resources, and implementation complexity. The choice of method depends on factors such as the tissue optical properties, source-detector separation, geometric complexity, and required output (e.g., fluence rate, radiance, or reflectance).

Near-infrared (NIR) light, occupying the spectral region from approximately 700 nm to 1700 nm, represents a critical optical window for biomedical applications. Within this range, light experiences minimized scattering, absorption, and autofluorescence in biological tissues, enabling deeper penetration and higher fidelity imaging and spectroscopy [27] [28]. This technical guide delineates the fundamental principles, current methodologies, and applications of NIR light in biomedical optics research, providing a framework for scientists and drug development professionals. The content is structured around the core NIR spectral divisions—NIR-I (700–900 nm) and NIR-II (1000–1700 nm)—and their respective roles in advancing non-invasive diagnostics, metabolic monitoring, and image-guided interventions.

Fundamental Principles of the Near-Infrared Window

The utility of the NIR window in biomedicine is governed by the interplay between light and tissue constituents. Key chromophores such as hemoglobin, water, and lipids exhibit distinct but manageable absorption profiles within the NIR range, allowing sufficient photon transmission for sensing and imaging. The reduced scattering coefficient relative to visible light facilitates penetration depths of several centimeters, a prerequisite for probing deep-tissue structures [27]. Furthermore, the NIR-II sub-window (1000–1350 nm) offers superior performance over NIR-I due to a more pronounced reduction in scattering and minimal autofluorescence, yielding enhanced spatial resolution and signal-to-background ratios for in vivo imaging [27].

Table 1: Characteristics of Near-Infrared Spectral Windows

Parameter	NIR-I (700–900 nm)	NIR-II (1000–1700 nm)	NIR-IIa (1000–1350 nm)
Penetration Depth	< 1 cm	Up to several centimeters	Optimal for deep-tissue imaging
Scattering	Moderate	Significantly Reduced	Minimized
Autofluorescence	Present	Negligible	Very Low
Water Absorption	Low	Moderate	Low (relative to 1350-1600 nm)
Key Applications	fNIRS, ICG imaging (clinical)	NIR-II fluorescence imaging, vascular mapping	High-resolution deep-tissue bioimaging

NIR Spectroscopy for Metabolic and Disease Monitoring

Near-infrared spectroscopy (NIRS) is a non-invasive, non-ionizing analytical technique that leverages the NIR window to quantify tissue composition and function.

Broadband NIRS for Cerebral Metabolism

Broadband NIRS (bNIRS) extends beyond conventional continuous-wave systems by employing a broad spectrum of light (typically 600-1000 nm) to resolve the concentration changes of cytochrome-c-oxidase (CCO), a key marker of mitochondrial metabolism and cellular energy status [29]. Despite its clinical potential, bNIRS adoption has been limited by instrumental complexity, cost, and size. Recent hardware developments cataloged over the past 37 years show a dominance of quartz tungsten halogen lamps and bench-top spectrometers, with a trend toward miniaturization using fiber optics and compact charge-coupled device sensors [29]. No fully commercial, portable bNIRS device currently exists, though micro form-factor spectrometers are paving the way for wearable designs [29].

Experimental Protocol for bNIRS Measurement of CCO:

• Instrument Setup: A typical system configuration involves a broadband light source (e.g., a quartz tungsten halogen lamp) and a spectrometer with a detection range of 600-1000 nm. Light is delivered to the scalp via a fiber-optic bundle.
• Data Acquisition: The diffusely reflected light is collected by a detector fiber and analyzed by the spectrometer, recording hundreds of wavelengths at each time sample.
• Spectral Analysis: Chromophore concentrations (oxyhemoglobin, deoxyhemoglobin, and oxidized CCO) are determined using spectroscopic algorithms, such as the UCLn algorithm, which employs a linear regression fit to the measured changes in optical density across the spectrum.
• Validation: Measurements are often validated against magnetic resonance spectroscopy (MRS), considered a benchmark for assessing cerebral metabolism [29].

NIRS in Conjunction with Machine Learning for Diagnostic Screening

NIRS, combined with machine learning (ML), presents a rapid, non-destructive alternative to traditional diagnostic methods like PCR. A proof-of-concept study for Hepatitis C virus (HCV) detection in serum samples utilized NIRS in the 1000–2500 nm range [30]. L1-regularized Logistic Regression identified informative wavelengths, which were then integrated with routine clinical markers (e.g., GPT, GOT, GGT) using a Random Forest model, achieving an accuracy of 72.2% and an AUC-ROC of 0.850 [30]. This highlights the potential of NIRS-ML integration for scalable, non-invasive early detection and risk assessment.

NIR Fluorescence Imaging

Fluorescence imaging in the NIR windows, particularly the NIR-II, has revolutionized pre-clinical in vivo visualization by providing deep-tissue penetration and high spatial resolution.

NIR-II Fluorescence Imaging with Organic Fluorophores

NIR-II fluorescence imaging (1000–1700 nm) is a focal point in tumor imaging due to its low scattering, weak autofluorescence, and high spatiotemporal resolution [27]. Organic small-molecule fluorophores are prominent owing to their superior biocompatibility, tunable optical properties, and predictable pharmacokinetics. Key structural archetypes include:

• Donor-Acceptor-Donor (D-A-D) frameworks: Featuring strong electron-withdrawing cores like benzobisthiadiazole (BBTD) for long-wavelength emission and high photostability [27].
• Cyanine derivatives: Characterized by a polymethine chain conjugated to terminal heterocycles [27].
• BODIPY and xanthene dyes: Noted for their excellent fluorescence quantum yields [27].

A significant clinical milestone was achieved in 2020, where NIR-II fluorescence-guided surgery using Indocyanine Green (ICG) was successfully performed on patients with liver cancer [27].

Table 2: Selected NIR-II Organic Small-Molecule Fluorophores and Properties

Fluorophore Class	Example Acceptor/Structure	Emission Range (nm)	Key Advantages
D-A-D	Benzobisthiadiazole (BBTD)	1000–1400	High photostability, tunable emission
Cyanine	IR-1061	1000–1300	High molar absorptivity
BODIPY	BODIPY FL	1000–1200	High quantum yield
Xanthene	Si-rhodamine	1000–1100	Excellent biocompatibility

Experimental Protocol for NIR-II Tumor Imaging:

• Probe Administration: The NIR-II fluorophore (e.g., ICG or a targeted organic small-molecule) is intravenously injected into the animal model or patient.
• Image Acquisition: At the appropriate time post-injection (to allow for background clearance and target accumulation), the subject is imaged using a NIR-II imaging system. This typically involves a NIR-II laser for excitation and an InGaAs camera for detection.
• Data Analysis: The acquired images are processed to quantify fluorescence intensity, determine tumor-to-background ratios, and delineate tumor margins.
• Guided Intervention: In surgical applications, the real-time NIR-II video feed assists in locating tumors and identifying critical vasculature [27] [28].

Advanced Microscopy Techniques

The evolution of optical sectioning microscopy techniques, such as light-sheet fluorescence microscopy (LSFM) and confocal/multiphoton microscopy adapted for the NIR-II window, has enabled high-resolution, volumetric imaging of living specimens with low phototoxicity [31] [28]. These methods are crucial for analyzing complex biological structures and functions within the brain and other organs.

The Scientist's Toolkit: Essential Research Reagents and Materials

Table 3: Key Reagents and Materials for NIR Biomedical Research

Item	Function/Application	Example/Note
Indocyanine Green (ICG)	Clinically approved NIR-I/NIR-II fluorophore for angiography and image-guided surgery.	FDA-approved; used in clinical NIR-II guided microsurgery [28].
Organic D-A-D Fluorophores	NIR-II imaging probes with tunable emission and good biocompatibility.	BBTD-based fluorophores; design focuses on reducing non-radiative decay [27].
Methylene Blue (MB)	NIR fluorophore investigated for intraoperative navigation of gastric tumors.	Shows specific uptake by gastric epithelial and cancer cells [28].
Quartz Tungsten Halogen Lamp	High-intensity broadband light source for bNIRS systems.	Dominant source in bNIRS developments [29].
InGaAs Camera	Detection of NIR-II fluorescence (1000-1700 nm).	Essential for NIR-II imaging systems [27].
Bench-top Spectrometer	Disperses and detects broadband light for bNIRS.	Common in laboratory systems; trend toward miniaturization [29].
Fiber Optics	Light delivery and collection for spectroscopy and imaging.	Enables flexible probe design for clinical and pre-clinical use [29] [32].
Targeted Molecular Probes	Fluorophores conjugated to targeting moieties (e.g., aptamers) for specific molecular imaging.	e.g., PD-L1 aptamer-anchored nanoparticles for imaging immune checkpoint expression [28].
S3QEL-2	S3QEL-2, MF:C19H25N5, MW:323.4 g/mol	Chemical Reagent
Cyclic(YCDGFYACYMDV)	Cyclic(YCDGFYACYMDV), MF:C65H82N12O20S3, MW:1447.6 g/mol	Chemical Reagent

The near-infrared spectral window provides an indispensable gateway for non-invasive optical interrogation of biological tissues. From monitoring cerebral metabolism with bNIRS to achieving high-resolution tumor visualization with NIR-II fluorophores, the applications are expanding rapidly. Future directions will focus on the miniaturization of hardware, the development of brighter and more specific contrast agents, and the deeper integration of multimodal data with machine learning algorithms. These advancements promise to further solidify the role of NIR optics in both basic biomedical research and clinical translation, ultimately enhancing diagnostic capabilities and therapeutic outcomes.

Biomedical Optical Imaging and Sensing: From Microscopy to Clinical Translation

Optical Coherence Tomography (OCT) is a non-invasive, label-free imaging technique that generates cross-sectional, micrometer-scale images of biological tissues using the backscattering properties of light [33]. First developed in 1991, OCT functions as the "optical equivalent of ultrasound" [34] [35], using near-infrared light waves instead of sound to create interferometric images. The core principle relies on low-coherence interferometry, where light from a broadband source is split into two paths: one directed toward the sample and the other toward a reference mirror [34]. The backscattered light from the sample is recombined with the reference light, and the resulting interference pattern is detected and analyzed to construct depth-resolved images [33]. This method allows for high-resolution visualization of tissue microstructure without the need for tissue excision or contrasting agents, making it particularly valuable for imaging delicate structures and dynamic processes.

The fundamental output of an OCT system is an A-scan (amplitude scan), which represents a single depth profile of reflectivity at one lateral position. A series of adjacent A-scans creates a B-scan (brightness scan), a two-dimensional cross-sectional image. Finally, multiple B-scans form a three-dimensional volumetric data set [34] [35]. A key advantage of OCT is its resolution, which typically ranges from 1-10 microns axially, bridging a critical gap between high-resolution (but shallow-penetrating) microscopy and deep-penetrating (but low-resolution) clinical imaging modalities like MRI and ultrasound [33]. This unique combination of capabilities has established OCT as an indispensable tool in biomedical optics research and clinical diagnostics.

Technical Implementations and System Architectures

Since its inception, OCT technology has evolved through several distinct generations, each offering improvements in speed, sensitivity, and image quality. The table below summarizes the key specifications of the primary OCT implementations.

Table 1: Technical Specifications of Major OCT Modalities

Parameter	Time-Domain OCT (TD-OCT)	Spectral-Domain OCT (SD-OCT)	Swept-Source OCT (SS-OCT)
Core Principle	Mechanically scans reference mirror depth; detects interference with a point detector [34] [35]	Uses spectrometer with fixed reference mirror; acquires entire depth profile simultaneously [34] [35]	Uses wavelength-sweeping laser and single detector; acquires spectral interferogram sequentially [34] [35]
Scanning Speed	~400 A-scans/second [35]	27,000-70,000 A-scans/second [35]	100,000-400,000 A-scans/second [35]
Axial Resolution	~10 µm [35]	5-7 µm [35]	~5 µm [35]
Light Source	Superluminescent Diode (810 nm) [35]	Broadband Superluminescent Diode (840 nm) [35]	Swept-Source Tunable Laser (1050 nm) [35]
Primary Clinical Use	Early retinal imaging [35]	Standard retinal and anterior segment imaging [35]	Deep tissue imaging (e.g., choroid) [35]

Fourier-Domain OCT (FD-OCT), which includes both SD-OCT and SS-OCT, represents the current standard for most applications. It offers a significant sensitivity and speed advantage over TD-OCT because it measures the interference spectrum as a function of wavelength, capturing the entire depth information in a single exposure without the need for mechanical scanning of the reference arm [34] [33]. This allows for dramatically faster image acquisition, which reduces motion artifacts and enables more complex volumetric imaging.

Optical Coherence Microscopy (OCM) is a high-resolution variant that combines the coherence gating of OCT with the confocal gating of a scanning microscope [33]. By using high-numerical-aperture objectives, OCM achieves superior lateral resolution, typically around 1-2 µm, which is suitable for visualizing individual cells. Full-Field OCT (FF-OCT) is another specialized implementation that employs a Linnik interferometer configuration with a broadband thermal light source and a 2D camera to capture en face images without the need for lateral scanning [36] [37]. This allows for high transverse resolution and simultaneous parallel detection of all points in the field of view, making it ideal for rapid, single-cell level morphological imaging, such as monitoring apoptosis and necrosis [36] [37].

Advanced Functional and Contrast-Enhanced Extensions

The basic structural imaging capabilities of OCT have been successfully extended to several functional modalities, providing insights into physiology, biomechanics, and molecular composition.

• OCT Angiography (OCTA): This functional extension visualizes blood flow by detecting motion contrast from circulating erythrocytes. By comparing the decorrelation signal between multiple rapidly acquired B-scans at the same location, OCTA can generate detailed, depth-resolved maps of the retinal and choroidal vasculature without the need for exogenous dye injection [38] [39] [35]. It has enabled the visualization of previously inaccessible capillary networks, including the radial peripapillary capillaries and the intermediate and deep capillary plexuses in the retina [38].

• Doppler OCT (D-OCT): This technique measures the Doppler frequency shift of backscattered light to quantitatively assess blood flow velocity [38] [33]. It is particularly useful for evaluating hemodynamics in larger vessels, though its sensitivity is angle-dependent.

• Polarization-Sensitive OCT (PS-OCT): PS-OCT measures the birefringence of tissues, which is altered in structures like collagen and nerve fiber bundles [33]. This provides contrast based on the tissue's microstructural arrangement and is valuable for assessing conditions like glaucoma or corneal scarring.

• Contrast-Enhanced OCT with Nanoparticles: To overcome the limited molecular contrast of conventional OCT, researchers have developed exogenous agents such as large gold nanorods (LGNRs). These agents exhibit a strong scattering cross-section and can be detected with picomolar sensitivity using specialized spectral detection algorithms, a method known as MOZART [40]. This allows for functional molecular imaging in vivo, such as mapping tumor microvasculature and lymphatic drainage patterns [40].

Table 2: Functional OCT Extension Modalities

Technique	Measured Parameter	Primary Application	Key Advantage
OCT Angiography (OCTA)	Motion contrast/decorrelation from blood flow [38] [35]	Mapping microvascular networks in retina, brain, skin [38] [39]	Non-invasive, depth-resolved visualization of capillaries without dyes
Doppler OCT (D-OCT)	Phase shift from moving scatterers [38] [33]	Quantitative blood flow velocity measurement [38]	Provides quantitative flow data
Polarization-Sensitive OCT (PS-OCT)	Tissue birefringence [33]	Imaging collagen, nerve fibers, muscle [33]	Contrast based on tissue micro-architecture
Contrast-Enhanced OCT	Spectral signal from nanoparticles (e.g., LGNRs) [40]	Molecular imaging, targeted contrast [40]	Enables molecular specificity in OCT

Experimental Protocols for High-Resolution Cellular Imaging

This section provides a detailed methodology for employing Full-Field OCT (FF-OCT) to monitor drug-induced morphological changes at the single-cell level, as exemplified by a 2025 study investigating apoptosis and necrosis [36] [37].

Research Reagent Solutions and Materials

Table 3: Essential Reagents and Materials for FF-OCT Cell Death Imaging

Item	Specification/Type	Function in Experiment
Cell Line	HeLa cells (human cervical cancer cells) [37]	A standard, well-characterized model system for in vitro studies.
Culture Medium	Dulbecco’s Modified Eagle’s Medium (DMEM) [37]	Provides nutrients and environment for cell growth and maintenance.
Apoptosis Inducer	Doxorubicin (5 μmol/L final concentration) [37]	Chemotherapeutic agent; intercalates into DNA, inducing programmed cell death.
Necrosis Inducer	Ethanol (99%) [37]	Causes nonspecific, rapid damage to cell membrane and proteins, inducing unregulated cell death.
Custom FF-OCT System	Time-domain Linnik interferometer with halogen light source (650 nm center wavelength) [37]	Enables label-free, high-resolution 3D imaging of cellular morphological dynamics.

Sample Preparation and Imaging Workflow

• Cell Culture and Seeding: HeLa cells are maintained as a monolayer in DMEM under standard culture conditions (37°C, 5% CO2). For experiments, cells are seeded onto appropriate imaging dishes and allowed to adhere and proliferate to the desired confluence [37].
• Induction of Cell Death:
  • Apoptosis Group: Replace the medium with DMEM containing 5 μmol/L doxorubicin. Doxorubicin triggers apoptosis by causing DNA double-strand breaks and increasing intracellular reactive oxygen species [37].
  • Necrosis Group: Replace the medium with DMEM containing 99% ethanol. Ethanol rapidly disrupts the phospholipid bilayer and denatures intracellular proteins, leading to loss of homeostasis and necrotic death [37].
• FF-OCT Image Acquisition:
  • Transfer the culture dish to the stage of the custom-built FF-OCT system.
  • The system utilizes a broadband halogen light source and identical 40x water-immersion objectives in a Linnik configuration to achieve sub-micrometer resolution [37].
  • Imaging is initiated immediately after drug administration. The precision linear stage controls the optical path length to position the coherence gate at specific cellular depths.
  • A CCD camera detects the 2D interference images. Phase-shifting via a piezoelectric actuator on the reference mirror is used to isolate the sample's reflection information [37].
  • To monitor dynamics, images are captured continuously at 20-minute intervals for up to 180 minutes. At each time point, a z-stack of en face images is acquired to enable 3D reconstruction and surface topography mapping [37].
• Data Processing and 3D Analysis:
  • The depth of maximum intensity for each pixel in the A-scan is identified as the cell surface.
  • These positions are mapped across the xy-plane to generate a 3D point cloud.
  • Spline interpolation is applied to reconstruct and analyze the volume and surface morphology of the cell structures [37].

The following workflow diagram summarizes the key experimental and imaging process.

Diagram 1: Experimental workflow for single-cell death imaging via FF-OCT.

Expected Morphological Outcomes

• Apoptotic Cells: Display characteristic, controlled changes including cell contraction, echinoid spine formation, membrane blebbing, and reorganization of filopodia [36] [37].
• Necrotic Cells: Exhibit rapid and disruptive events such as immediate membrane rupture, leakage of intracellular contents, and an abrupt loss of adhesion structures [36] [37].

FF-OCT-based interference reflection microscopy (IRM)-like imaging effectively highlights the changes in cell-substrate adhesion and boundary integrity throughout these processes [36].

Applications in Biomedical Research and Clinical Translation

OCT and OCM have established profound utility across a wide spectrum of biomedical fields, from basic research to clinical diagnostics and therapeutic monitoring.

In ophthalmology, OCT is the standard of care for diagnosing and managing retinal diseases. It provides critical structural information for conditions like macular holes, epiretinal membranes, age-related macular degeneration, diabetic retinopathy, and glaucoma [34] [39] [35]. The integration of OCT with scanning laser ophthalmoscopy allows for precise motion tracking and the ability to re-scan the exact same retinal location during follow-up visits, enabling meticulous therapy control [34]. Furthermore, the segmentation of retinal layers provides objective, quantitative biomarkers, such as the thickness of the retinal nerve fiber layer for glaucoma diagnosis [34] [35].

In neuroscience and neurology, OCT is used for both basic research and clinical applications. In rodent models, it enables in vivo, label-free imaging of the cerebral cortex and microvasculature at high resolution [33]. Clinically, retinal imaging with OCT serves as a window to the brain. Since the retina is an extension of the central nervous system, thinning of the retinal nerve fiber layer, as measured by OCT, can serve as a biomarker for the progression of neurodegenerative diseases like multiple sclerosis and Alzheimer's disease [33].

In oncology and drug development, the high-resolution morphological imaging capabilities of OCT and FF-OCT are invaluable. As demonstrated in the experimental protocol, FF-OCT can distinguish between different modes of cell death (apoptosis vs. necrosis) in response to chemotherapeutic agents (e.g., doxorubicin) or toxic insults [36] [37]. This provides a powerful, label-free platform for drug toxicity testing and anti-cancer therapy evaluation in vitro. The development of contrast-enhanced OCT with targeted nanoparticles (MOZART) further opens the door to molecular imaging of tumor vasculature and specific biomarkers in vivo [40].

The following diagram illustrates the core principle of OCT's signal generation and processing.

Diagram 2: Core principle of OCT signal generation via interferometry.

Recent innovations continue to expand OCT's capabilities. Visible-light OCT enables high-resolution structural imaging combined with retinal oximetry [39]. Optoretinography (ORG) detects stimulus-evoked intrinsic optical signals from photoreceptors, potentially replacing electroretinography for objective functional assessment [39]. Furthermore, efforts in portable and accessible OCT design aim to decentralize this technology, bringing it into community clinics for wider screening and remote surveillance of chronic diseases [41]. The integration of artificial intelligence (AI) and deep learning for automated analysis of OCT images is also becoming widespread, enhancing diagnostic accuracy and providing human-level performance in detecting conditions like glaucoma [39].

Functional and molecular imaging represents a paradigm shift in biomedical optics, enabling researchers to visualize not only anatomical structure but also physiological activity and molecular-level processes. Within this domain, Optical Coherence Tomography (OCT) has evolved from a purely structural imaging technique to a versatile platform for functional assessment. The integration of Doppler principles with OCT has unlocked capabilities for quantifying flow dynamics, while OCT angiography (OCTA) has revolutionized microvascular imaging. Concurrently, the development of advanced molecular probes has created pathways for targeted molecular imaging, opening new frontiers in drug development and basic research. This technical guide examines the core principles, methodologies, and applications of these technologies within the broader context of biomedical optics research, providing researchers and drug development professionals with a comprehensive framework for their implementation.

Core Principles of Doppler OCT

Doppler OCT is a functional extension of OCT that enables quantification of particle flow speed with high spatial resolution and sensitivity alongside structural imaging [42]. First demonstrated in 1997, Doppler OCT fundamentally relies on the Doppler principle, where the frequency of backscattered light from moving particles undergoes a shift proportional to their velocity [42] [43].

Fundamental Doppler Physics

The Doppler frequency shift (Δf) is calculated using the wave vectors of incoming (kᵢ) and scattered (kₛ) light, and the velocity vector (V) of moving particles [42]:

Δf = (1/2π)(kₛ - kᵢ) · V

When considering the Doppler angle θ (between incident light beam and flow direction), this equation simplifies to:

Δf = (2 · n · V · cos(θ))/λ

where n is the tissue refractive index and λ is the central wavelength of the light source [42]. This relationship forms the foundation for all Doppler OCT velocity measurements.

Evolution of Doppler OCT Methods

The development of Fourier-domain OCT significantly enhanced imaging speed and paved the way for more sophisticated Doppler techniques [42]. The table below summarizes the key methodological developments in Doppler OCT:

Table 1: Evolution of Doppler OCT Methodologies

Method	Principle	Advantages	Limitations
Spectrogram Analysis	Short-time FFT or wavelet transformation to extract Doppler shift from power spectrum [42]	Simultaneous structural and velocity imaging [42]	Compromised velocity sensitivity with increased spatial resolution/speed [42]
Phase-Resolved Doppler OCT	Calculates phase change between sequential A-lines [42] [43]	High velocity sensitivity, spatial resolution, and imaging speed simultaneously [42]	Sensitive to flow orientation; ineffective at ~90° Doppler angle [42]
Doppler Variance OCT	Utilizes Doppler bandwidth to quantify flow [42]	Effective for transverse flow; enables capillary-level visualization [42]	Limited by phase wrapping and washout at extreme velocities [42]

The phase-resolved method represents a significant advancement, where Doppler shift is derived through phase change between sequential A-lines [42]:

Δf = Δφ/(2 · π · ΔT)

where ΔT is the time interval between sequential A-lines, and Δφ is the phase change calculated from OCT complex data (Fₘ and Fₘ₊₁) [42]:

Δφ = tan⁻¹[Im(Fₘ × Fₘ₊₁)/Re(Fₘ × Fₘ₊₁)]

This enables calculation of longitudinal flow velocity [42]:

V · cos(θ) = (λ · Δφ)/(4 · π · n · ΔT)

OCT Angiography (OCTA): Principles and Applications

OCTA represents a specialized application of Doppler principles that reconstructs microvasculature by detecting micro-motions induced by moving blood cells and plasma [42]. These motions generate fluctuations in the amplitude and phase of interference signals that correlate with flow velocity.

Technical Foundations of OCTA

The first OCTA based on Doppler variance was demonstrated in 2001, with subsequent development of various algorithms detecting fluctuations in amplitude and/or phase [42]. OCTA provides exceptional resolution (1-15 μm) with moderate penetration depth (1-2 mm), offering significant advantages over conventional angiography methods including non-invasiveness, depth-resolved information, and absolute flow measurement [42].

Comparative Analysis of Angiography Modalities

Table 2: Performance Comparison of Angiography Modalities

Method	Lateral Resolution	Axial Resolution	Flow Velocity Sensitivity	Invasiveness
ICG Angiogram	Good	None	None	Yes [42]
Laser Doppler Flowmetry	Good	None	Moderate	None [42]
Doppler Ultrasound	Moderate	Moderate	Good	None [42]
Laser Speckle	Good	None	Moderate	None [42]
Doppler OCT/OCTA	Good	Good	Good	None [42]

Clinical and Research Applications

Recent advances in OCTA have demonstrated particular utility in ophthalmology and vascular monitoring. A 2025 study investigated the correlation between internal carotid artery stenosis (ICAS) and retinal microvascular changes in hypertensive patients, analyzing vascular measurements from OCTA and carotid Doppler ultrasonography [44]. The research found statistically significant correlations between carotid Doppler velocities and OCTA parameters including vascular flow area (VFA) and non-flow area (NFA), suggesting OCTA's potential for monitoring microvascular changes associated with carotid stenosis [44].

Additionally, 2025 research demonstrated point-of-care widefield retinal OCTA mosaicking using a handheld spectrally encoded coherence tomography and reflectometry probe, highlighting the trend toward portable, high-throughput OCTA systems for capillary-resolution imaging [45].

Molecular Probes for Bioimaging and Biosensing

Molecular probes represent a complementary technology to functional OCT, enabling specific detection of biological targets and processes through optical imaging.

Probe Diversity and Design Principles

Fluorescent probe-based techniques are recognized as powerful tools for real-time imaging and sensing in biological samples, capable of detecting species including metal ions, reactive oxygen species, and metabolites, while also probing microenvironmental parameters like pH and viscosity [46]. Numerous fluorescence agents have been developed, including:

• Organic fluorophores: Small molecule dyes with tunable properties
• Genetically encodable probes: Fluorescent proteins and biological constructs
• Nanoparticle probes: Quantum dots and other nanoscale emitters
• Supramolecular fluorophores: Assemblies with emergent optical properties [46]

Effective probe design involves regulating electronic and spectral characteristics to achieve high selectivity and specific functionality, with advanced probes offering enhanced tissue penetration, reduced autofluorescence, improved photostability, and multi-modal imaging capabilities [46].

Advanced Probe Development and Applications

Recent innovations in molecular probes include iridium(III) complex-based luminogenic probes for high-throughput screening of hydrogen sulfide donors in living cells, enabling anti-interference screening capable of distinguishing target signals from complex background autofluorescence [46]. Additionally, two-photon fluorescence probes for norepinephrine biosensing on a 100ms timescale permit precise monitoring of neurotransmitter dynamics with high spatiotemporal resolution in living systems [46].

The expanding repertoire of near-infrared-II (NIR-II) fluorophores with emission extending to 1900nm enables in vivo imaging of deep tissues with enhanced signal-to-background ratios, while bioorthogonally activatable cyanine dyes based on "torsion-induced disaggregation" allow sensitive in vivo tumor imaging through controlled fluorescence activation [46].

Experimental Protocols and Methodologies

Phase-Resolved Doppler OCT Protocol

Sample Preparation:

• For phantom studies: Utilize membrane-resembling materials with controlled vibration properties
• For biological specimens: Prepare tissue samples with appropriate physiological maintenance
• For in vivo applications: Implement anesthetic protocols and motion stabilization

Instrumentation Setup:

• Configure Fourier-domain OCT system with appropriate wavelength source (typically 800-1300nm)
• Calibrate phase stability and scanning parameters
• Implement resonant scanner or similar high-speed scanning mechanism for dynamic imaging

Data Acquisition:

• Acquire sequential B-scans at same position for Doppler analysis
• Set A-line rate appropriate for expected velocity range (typically 10-100kHz)
• Maintain adequate beam spacing for spatial resolution requirements

Signal Processing:

• Apply phase-resolved algorithm to calculate Doppler shift between consecutive A-lines
• Implement phase unwrapping algorithms to address velocity ambiguities
• Utilize averaging masks (typically 4-8 A-lines) to enhance SNR while maintaining resolution
• Apply directional filtering to separate forward and reverse flow components

Validation:

• Correlate with known flow rates in phantom systems
• Compare with alternative velocimetry methods where feasible
• Perform statistical analysis of measurement reproducibility [42] [43]

OCTA Imaging Protocol

Subject Preparation:

• For ophthalmic applications: Employ pupil dilation as needed
• For dermatological applications: Clean imaging area and minimize pressure artifacts
• Position subject to minimize motion artifacts during acquisition

Image Acquisition:

• Acquire repeated B-scans or volumetric stacks at same position
• Optimize scan pattern density for adequate lateral sampling
• Adjust integration time to balance signal strength and motion artifacts

Angiogram Processing:

• Calculate decorrelation or variance between repeated scans
• Apply segmentation algorithms to separate vascular layers
• Remove motion artifacts using registration algorithms
• Apply noise reduction filters while preserving vascular details

Quantitative Analysis:

• Calculate vessel density metrics from binarized angiograms
• Determine fractal dimension for vascular complexity assessment
• Quantify flow indices based on decorrelation values
• Perform statistical comparison with control groups [42] [44] [45]

Molecular Probe Validation Protocol

Probe Characterization:

• Measure absorption and emission spectra in relevant solvents
• Determine quantum yield and brightness under physiological conditions
• Assess photostability under continuous illumination

Specificity Validation:

• Test response to target analyte versus potential interferents
• Determine limit of detection and dynamic range
• Assess binding affinity and kinetics where applicable

Cellular Validation:

• Evaluate cellular uptake and subcellular localization
• Assess cytotoxicity through viability assays
• Verify target engagement through pharmacological or genetic manipulation

In Vivo Validation:

• Determine pharmacokinetics and biodistribution
• Establish optimal dosing and imaging time windows
• Validate specificity through control probes or competition experiments [46]

Visualization of Doppler OCT Principles

Diagram 1: Doppler OCT conceptual framework showing fundamental principles, methodological approaches, and functional applications.

Research Reagent Solutions

Table 3: Essential Research Reagents and Materials for Functional and Molecular Imaging

Reagent/Material	Function	Application Examples
Iridium(III) complex-based probes	Luminogenic detection of mitochondrial Hâ‚‚S	High-throughput screening of hydrogen sulfide donors in living cells [46]
NIR-II fluorophores	Deep tissue imaging with reduced scattering	In vivo imaging with emission up to 1900nm for enhanced signal-to-background ratios [46]
Bioorthogonal activatable dyes	Turn-on fluorescence via specific chemical reactions	Sensitive in vivo tumor imaging through "torsion-induced disaggregation" [46]
Stochastic multicolor labeling kits	Multiplexed neuronal tracing	Automated neurite reconstruction via unsupervised clustering of color information [46]
FRET-based peptide probes	Protease activity sensing	Detection of Cathepsin D activity in macrophages during immune response [46]
Phase mask algorithms	Doppler signal processing	Enhancement of SNR in phase-resolved Doppler OCT [43]
Autocorrelation processing tools	Doppler variance calculation	Transverse flow quantification in Doppler variance OCT [42]

The convergence of Doppler OCT, OCT angiography, and molecular probe technologies represents a powerful trend in biomedical optics research, enabling comprehensive assessment of structure, function, and molecular composition in biological systems. Doppler OCT provides robust methodologies for quantifying flow dynamics and tissue biomechanics, while OCTA offers exceptional resolution for visualizing microvascular networks without exogenous contrast agents. Molecular probes complement these techniques by enabling specific detection of biochemical processes and targets. For researchers and drug development professionals, understanding the principles, capabilities, and limitations of these technologies is essential for designing effective studies and interpreting complex biomedical data. As these fields continue to evolve, particularly with integration of artificial intelligence and multimodal approaches, they promise to deliver increasingly sophisticated tools for basic research and clinical translation.

Near-infrared spectroscopy (NIRS) and diffuse optical tomography (DOT) are non-invasive biomedical optical techniques that utilize light in the near-infrared (NIR) range (approximately 700-950 nm) to probe the optical properties of biological tissues. Biological tissue is relatively transparent in this specific "optical window" because the primary tissue chromophores—water, hemoglobin, and lipids—exhibit low absorption coefficients in this region [47]. This physical characteristic enables NIR light to penetrate biological tissue to depths of several centimeters, facilitating the assessment of both tissue structure and function.

NIRS originally emerged as a tool for qualitative monitoring of hemodynamic changes by measuring concentration changes in oxygenated and deoxygenated hemoglobin (oxy-Hb and deoxy-Hb) [47]. The technology has since evolved into a powerful neuroimaging modality known as functional NIRS (fNIRS). In parallel, DOT was developed as an extension of NIRS, employing multiple source-detector pairs and image reconstruction algorithms to generate cross-sectional or volumetric images of optical properties within highly scattering media [48] [47]. While DOT typically offers lower spatial resolution compared to modalities like MRI or CT, it provides unique advantages including sub-second temporal resolution for imaging hemodynamics and other fast-changing processes, compact portable instrumentation for bedside monitoring, and access to physiologically relevant parameters not easily accessible with other techniques [48].

Technical Foundations of NIRS and DOT

Light-Tissue Interaction and Propagation Models

The interaction between NIR light and biological tissue is dominated by absorption and scattering phenomena. Absorption depends on the concentration and type of chromophores present, while scattering occurs due to variations in refractive index within the tissue microstructure. In biological tissue, scattering is generally dominant over absorption, and the scattering is highly anisotropic, preferentially in the forward direction [47].

Two principal models describe light propagation in tissue:

• Radiative Transfer Equation (RTE): Widely accepted as the most accurate model, the RTE is an energy conservation equation for light propagation through media with absorbers and scatterers. It is an integro-differential equation that is computationally intensive to solve [47].
• Diffusion Equation (DE): For optically thick media where multiple scattering occurs, the light fluence becomes almost isotropic. The DE is a simplification derived from the RTE under the P1 approximation (approximating the intensity by the first two terms of a spherical harmonics expansion). It is expressed as: [ \left [ \frac{\partial}{v(r)\partial t} - D\nabla^2 + \mua(r) \right ] \Phi(r,t) = q(r,t) ] where ( \Phi(r,t) ) is the fluence rate, ( D ) is the diffusion coefficient ( [3(1-g)\mus(r)]^{-1} ), ( \mua ) is the absorption coefficient, ( \mus ) is the scattering coefficient, ( g ) is the anisotropic factor, ( v ) is the velocity of light, and ( q ) is the isotropic source [47]. The term ( (1-g)\mus ) is the reduced scattering coefficient (( \mus' )).

Measurement Techniques and Instrumentation

NIRS and DOT instruments can be categorized into three primary measurement types, each with distinct operational principles and capabilities [47]:

• Continuous Wave (CW): The most common and cost-effective approach. CW instruments use light sources at constant intensity and measure the attenuated intensity of transmitted or back-scattered light. They typically apply the Modified Beer-Lambert Law (MBLL) to relate attenuation changes to concentration changes: ( A = -\log I/I0 = \epsilon CL + S ), where ( A ) is attenuation, ( I ) and ( I0 ) are detected and incident intensities, ( \epsilon ) is the molar absorption coefficient, ( C ) is chromophore concentration, ( L ) is the mean optical pathlength, and ( S ) is attenuation due to scattering [47]. A key limitation is that CW systems cannot directly measure the absolute pathlength ( L ), thus typically providing only relative concentration changes.
• Frequency Domain (FD): These systems modulate the light source at radio frequencies (e.g., ~100 MHz). They measure the amplitude decay, phase shift, and average intensity of the detected light. The phase shift provides information to calculate the mean photon time-of-flight, enabling the determination of absolute optical properties and chromophore concentrations.
• Time Domain (TD): Also known as Time-Resolved Spectroscopy (TRS), TD systems use short picosecond light pulses. They measure the temporal dispersion (temporal point spread function) of the pulse after traveling through tissue. This provides the most comprehensive information, allowing direct quantification of absorption and scattering coefficients and absolute concentrations of tissue chromophores.

Diagram 1: Experimental workflow for NIRS and DOT, showing the three primary measurement techniques.

From NIRS to Diffuse Optical Tomography

While single-channel NIRS provides a localized hemodynamic measurement, DOT extends this concept to tomographic imaging. DOT utilizes multiple source and detector optodes arranged in specific geometries around the tissue of interest (e.g., head, breast, limb). By measuring the light propagation between multiple source-detector pairs and applying sophisticated image reconstruction algorithms based on the diffusion equation or RTE, DOT can reconstruct the internal spatial distribution of absorption and scattering coefficients [48] [47].

A critical concept in DOT image reconstruction is the photon measurement density function, which describes the spatial sensitivity of a given source-detector pair to changes in optical properties within the tissue. The region of highest sensitivity between a source and detector is often described as having a banana-shaped profile in the reflectance geometry, with maximum sensitivity extending beneath the surface [49]. The spatial resolution of DOT is inherently limited by strong light scattering but is typically on the order of ~1 cm within the imaging domain.

Table 1: Key Parameters in NIRS and DOT Light Propagation

Parameter	Symbol	Description	Typical Range in Tissue
Absorption Coefficient	(\mu_a)	Probability of absorption per unit path length. Determined by chromophore concentrations.	0.01 - 0.1 cm⁻¹ (NIR window)
Reduced Scattering Coefficient	(\mu_s')	Effective probability of isotropic scattering per unit path length. ( \mus' = (1-g)\mus ).	5 - 20 cm⁻¹ (NIR window)
Anisotropy Factor	(g)	Average cosine of the scattering angle. Describes scattering directionality.	~0.9 (highly forward-scattering)
Fluence Rate	(\Phi)	Total light power incident from all directions onto a small sphere, per unit cross-sectional area.	-

Clinical and Research Applications

Functional Brain Imaging

Functional brain imaging is a primary application of NIRS and DOT. Neural activation triggers a localized hemodynamic response, increasing cerebral blood flow and altering the concentrations of oxy-Hb and deoxy-Hb. NIRS and DOT can track these changes with high temporal resolution (potentially sub-second) [48]. Studies comparing NIRS with the gold-standard functional MRI (fMRI) have found that NIRS signals, particularly oxy-Hb, are often highly correlated with the BOLD response, despite NIRS having a weaker signal-to-noise ratio and poorer spatial resolution [49]. DOT improves upon conventional NIRS by providing better depth discrimination and 3D localization of brain activity, helping to distinguish cortical signals from confounding hemodynamic changes in the scalp [47]. Applications include mapping sensorimotor, visual, and cognitive functions, monitoring bedside cerebral oxygenation in critically ill patients, and studying neurovascular coupling.

Breast Imaging and Oncology

DOT shows significant promise in breast imaging, particularly for monitoring neoadjuvant chemotherapy response and for differentiating benign from malignant lesions. Tumors often exhibit elevated absorption due to increased vascularity and hemoglobin concentration. DOT can provide functional information about tumor hypoxia and metabolic rate, complementing anatomical imaging modalities like X-ray mammography and MRI. The technique is non-ionizing, making it suitable for repeated monitoring over time.

Musculoskeletal and Joint Imaging

NIRS and DOT are used to assess muscle oxygenation and hemodynamics during exercise and in pathological conditions. Applications include monitoring rehabilitation progress, diagnosing peripheral arterial disease, and investigating muscle metabolism in athletes. Joint imaging, particularly for inflammatory arthritis like rheumatoid arthritis, can detect synovial inflammation and hypervascularity, potentially aiding in diagnosis and treatment monitoring [48].

Emerging Applications and Guidance

The U.S. Food and Drug Administration (FDA) has recognized the potential of optical imaging, issuing guidance for the development of optical imaging drugs. These are often used as intraoperative aids for detecting pathology such as tumors or for enhancing the conspicuity of normal anatomical structures [50]. Furthermore, the development of handheld NIRS spectrometers is expanding the technology into new areas such as material identification, food authentication, and environmental investigations, demonstrating the versatility of the underlying technology [51].

Table 2: Comparison of NIRS/DOT with Other Neuroimaging Modalities

Feature	NIRS/DOT	fMRI	EEG/MEG
Spatial Resolution	Low (~1 cm)	High (1-3 mm)	Low-High (depending on source model)
Temporal Resolution	High (sub-second)	Low (1-2 s)	Very High (milliseconds)
Measured Signal	Hemodynamics (HbO/HbR)	Blood oxygenation (BOLD)	Electrical/Magnetic neuronal activity
Portability	High (bedside systems available)	Low	Medium (EEG) to Low (MEG)
Cost	Relatively low	High	Medium-High
Patient Tolerance	High (silent, non-confining)	Moderate (loud, confined)	High

The Scientist's Toolkit: Essential Reagents and Materials

Successful implementation of NIRS and DOT experiments requires specific tools and reagents. The following table details key components of a typical research setup.

Table 3: Key Research Reagent Solutions and Materials for NIRS/DOT

Item	Function / Description	Application Notes
NIR Light Sources	Emits light in the 650-950 nm optical window. Common types: laser diodes, light-emitting diodes (LEDs).	Lasers offer higher power; LEDs are cheaper and robust. Wavelengths typically ~690, 780, 830 nm for HbO/HbR discrimination.
NIR Detectors	Measures light intensity after tissue propagation. Common types: photomultiplier tubes (PMTs), avalanche photodiodes (APDs), silicon/InGaAs photodiodes.	Choice depends on measurement type (CW/FD/TD). PMTs/APDs are sensitive for TD/FD; InGaAs is standard for NIR range in CW systems.
Optode Probes	Hardware interfaces containing source and detector fibers that make contact with the tissue surface.	Design (e.g., distance between source-detector pairs) determines sensitivity and penetration depth.
Optical Phantoms	Tissue-simulating materials with calibrated optical properties (( \mua ), ( \mus' )).	Used for system validation, calibration, and testing reconstruction algorithms. Often made from epoxy, resin, or gels with Intralipid (scatterer) and ink (absorber).
Head Probe Caps	Flexible caps or grids with pre-determined holes for holding optodes in place on the scalp.	Essential for reproducible probe placement across subjects and sessions in brain imaging studies (fNIRS).
3D Digitizer	Electromagnetic or optical system to record the 3D spatial coordinates of optodes on the subject.	Crucial for co-registering NIRS/DOT data with anatomical images (e.g., MRI) for accurate spatial interpretation.
Dapsone-13C12	Dapsone-13C12, CAS:1632119-29-9, MF:C12H12N2O2S, MW:260.22 g/mol	Chemical Reagent
TKL-IN-2	TKL-IN-2, MF:C23H17ClF3N3O, MW:443.8 g/mol	Chemical Reagent

Experimental Protocol: A Representative fNIRS Brain Activation Study

This protocol outlines a standard block-design functional NIRS experiment to measure cortical activation during a motor task.

Aim: To measure hemodynamic changes in the primary motor cortex (M1) contralateral to finger movement.

Materials and Setup:

• A continuous-wave (CW) fNIRS system with a minimum of two wavelengths (e.g., 760 nm and 850 nm).
• A probe set containing multiple source-detector pairs (channels). The source-detector separation should be 2.5-3.5 cm to ensure sufficient penetration into the cortical tissue.
• A flexible cap to securely hold the probes over the motor cortex.
• A 3D digitizer to record probe locations.
• A computer for stimulus presentation and task synchronization.

Procedure:

• Subject Preparation: Obtain informed consent. Position the subject comfortably in a chair. Place the fNIRS cap on the subject's head, aligning the probe holder over the C3/C4 positions (International 10-20 system) for left/right motor cortex.
• Probe Placement and Co-registration: Secure the fNIRS probes into the cap. Use the 3D digitizer to record the 3D coordinates of every source and detector optode relative to anatomical landmarks (nasion, inion, pre-auricular points).
• Signal Quality Check: Start data acquisition and visually inspect the raw light intensity signals for each channel. Ensure signals are stable and free from excessive motion artifact or low signal-to-noise ratio. Adjust probe contact if necessary.
• Experimental Paradigm: Implement a block design.
  • Resting Baseline (e.g., 30 s): Subject remains still, fixating on a cross.
  • Task Block (e.g., 20 s): Subject performs repetitive finger tapping with their right hand at a self-paced rate.
  • Repeat the Rest/Task cycle for a minimum of 5-10 repetitions.
• Data Acquisition: Record fNIRS data continuously throughout the experiment, simultaneously with triggers marking the onset and offset of each task block.

Data Processing and Analysis:

• Preprocessing: Convert raw light intensity to optical density. Apply band-pass filtering (e.g., 0.01 - 0.2 Hz) to remove cardiac pulsation, respiration, and very slow drifts.
• Hemodynamic Conversion: Use the Modified Beer-Lambert Law (MBLL) to convert the filtered optical density changes at two wavelengths into concentration changes for oxy-hemoglobin (Δ[HbO]) and deoxy-hemoglobin (Δ[HbR]).
• General Linear Model (GLM) Analysis: For each channel, model the hemodynamic response using a GLM. The design matrix is convolved with a canonical hemodynamic response function based on the task timing.
• Statistical Mapping: Generate statistical parametric maps (e.g., t-maps) for Δ[HbO] and Δ[HbR]. The channel over the left motor cortex is expected to show a significant increase in Δ[HbO] and a decrease in Δ[HbR] during the right-hand tapping task compared to rest.

Diagram 2: The probabilistic path of a single photon during NIRS measurement, dominated by scattering events.

Current Challenges and Future Directions

Despite its advantages, NIRS/DOT faces several challenges. The technology suffers from a relatively poor spatial resolution and limited penetration depth (a few centimeters). The image reconstruction problem is inherently ill-posed and non-linear, meaning small errors in measurements can lead to significant errors in the reconstructed images. Furthermore, accurately modeling light propagation in complex, layered tissues (e.g., head with scalp, skull, CSF, and brain) remains difficult [47].

Future developments are focused on several key areas:

• High-Density DOT (HD-DOT): Using dense arrays of source-detector pairs to significantly improve spatial resolution and image quality, approaching that of fMRI for cortical mapping [52].
• Multimodal Integration: Combining NIRS/DOT with other modalities like EEG, fMRI, or MEG to leverage the complementary strengths of each technique (e.g., high temporal resolution from EEG with hemodynamic information from DOT).
• Advanced Modeling and AI: Incorporating more realistic anatomical priors from MRI into light propagation models and employing machine learning and artificial intelligence for improved image reconstruction and data analysis [53].
• Miniaturization and Wearable Systems: The development of compact, portable, and even handheld NIRS devices is expanding applications into real-world environments and point-of-care diagnostics [51].
• Standardization and Commercialization: Efforts by organizations like the Society for functional NIRS (SfNIRS) and regulatory bodies like the FDA are helping to standardize practices and guide the translation of these technologies from the lab to the clinic [50] [52].

Photoacoustic Tomography (PAT) is a rapidly growing hybrid biomedical imaging modality that combines rich optical absorption contrast with the high resolution and penetration depth of ultrasound imaging. By acoustically detecting optical absorption, PAT bridges the gap between microscopic optical imaging and macroscopic clinical imaging, providing a consistent contrast mechanism across spatial scales. This technical guide details the core principles, major implementations, and integration of PAT within multimodal systems, providing a foundation for its application in biomedical optics research and drug development.

Core Principles of Photoacoustic Tomography

The fundamental principle of PAT is the photoacoustic effect, where absorbed optical energy is converted into acoustic energy [54] [55]. The imaging process involves several key stages:

Signal Generation and Physics

When a short-pulsed laser (typically nanosecond duration) illuminates biological tissue, photons propagate and are absorbed by chromophores such as hemoglobin, melanin, or exogenous contrast agents [55]. The absorbed energy is converted into heat, leading to a localized thermoelastic expansion and the generation of a broadband ultrasonic wave, the photoacoustic (PA) signal [54].

• Thermal and Stress Confinement: For efficient PA signal generation, the laser pulse width must be shorter than both the thermal relaxation time (( \tau{th} )) and the stress relaxation time (( \taus )) of the targeted tissue voxel [54]. This ensures that heat conduction and volume expansion during the laser pulse are negligible, confining the thermal energy and resulting in strong pressure generation.
• Initial Pressure Rise: The initial pressure rise (( p0 )) at the absorption site is the source of the acoustic signal and is described by: ( p0 = \Gamma \eta{th} \mua F ) where:
  • ( \Gamma ) is the Grueneisen parameter, a dimensionless thermodynamic constant [54].
  • ( \eta{th} ) is the percentage of absorbed energy converted to heat [54].
  • ( \mua ) is the optical absorption coefficient (cm⁻¹) [54].
  • ( F ) is the local optical fluence (J/cm²) [54].

This equation shows that the PA signal is directly proportional to the optical absorption coefficient, providing 100% relative sensitivity to small absorption variations [55].

Wave Propagation and Detection

The initial pressure ( p0 ) propagates through the tissue as an ultrasonic wave. This propagation in an inviscid medium is governed by the following wave equation [54]: [ (\nabla^2 - \frac{1}{vs^2} \frac{\partial^2}{\partial t^2})p(\vec{r},t) = -\frac{\beta}{Cp} \frac{\partial H(\vec{r},t)}{\partial t} ] where ( vs ) is the speed of sound, ( \beta ) is the volumetric thermal expansion coefficient, ( Cp ) is the specific heat capacity, and ( H ) is the heating function representing the thermal energy deposited per unit volume and time [54]. These PA waves, which scatter much less than light in biological tissue, are then detected by ultrasonic transducers placed outside the tissue [56]. The goal of PAT is to reconstruct the original distribution of ( p0 ), which maps the optical absorption, from the detected time-resolved acoustic signals [54].

The following diagram illustrates the core principle and the two primary image formation methods in PAT:

Major PAT Implementations and System Characteristics

PAT is implemented primarily through two image formation methods, each with distinct system configurations and performance characteristics suited to different research needs.

Photoacoustic Computed Tomography (PACT)

PACT uses wide-field light illumination to excite a large tissue area. The resulting PA waves are detected at multiple locations around the object using an ultrasonic transducer array or a scanned single-element transducer [55] [56]. An image of the initial pressure distribution is then reconstructed mathematically.

• Reconstruction Algorithms: Common algorithms include the Universal Back-Projection (UBP) and the Time-Reversal method [54]. UBP is faster but assumes an acoustically homogeneous medium, while time-reversal can account for acoustic heterogeneities but is computationally intensive [54].
• Deep Learning Reconstruction: To address challenges like sparse sensing or limited-view detection, deep learning-based reconstruction methods have been developed. These include learning-based post-processing of direct reconstructions and model-based learned iterative reconstruction, which integrates the physical model into the network and has shown superior generalizability and robustness [57].

Photoacoustic Microscopy (PAM)

PAM forms an image through mechanical raster-scanning of a confocally aligned optical excitation and acoustically focused single-element ultrasonic transducer [55] [56]. The axial resolution is determined by the bandwidth of the ultrasonic transducer, while the lateral resolution is determined by the tightest focus, either optical or acoustic.

• Optical-Resolution PAM (OR-PAM): Employs a tightly focused laser beam, providing a lateral resolution at the micron scale, but penetration is limited to about 1 mm due to optical scattering [55].
• Acoustic-Resolution PAM (AR-PAM): Uses a diffused optical beam and a tightly focused ultrasonic transducer. The lateral resolution is acoustically determined, typically tens to hundreds of microns, enabling deeper penetration of several millimeters [55].

The performance characteristics of these major implementations are summarized in the table below.

Table 1: Characteristics of Major PAT Implementations [55] [56]

Feature	Photoacoustic Computed Tomography (PACT)	Photoacoustic Microscopy (PAM)
Illumination & Detection	Wide-field illumination; detection via array or scanning single-element transducer.	Raster-scanning of confocally aligned optical and acoustic foci.
Primary Resolution	Resolution is reconstruction-dependent and can be nearly isotropic.	OR-PAM: Optically determined lateral resolution.AR-PAM: Acoustically determined lateral resolution.
Typical Spatial Resolution	Tens to hundreds of micrometers.	OR-PAM: Sub-micron to a few microns.AR-PAM: Tens of microns.
Penetration Depth	Up to several centimeters.	OR-PAM: ~1 mm.AR-PAM: A few millimeters.
Imaging Speed	High (single-pulse can generate a 2D/3D image).	Lower (limited by scanning speed).
Key Applications	Whole-organ or small-animal imaging; brain functional imaging; breast imaging.	Microvasculature imaging; dermatology; ophthalmology.

PAT in Multimodal Systems

A key strength of PAT is its inherent compatibility with other imaging modalities. By providing complementary contrast mechanisms, multimodal systems enable a more comprehensive characterization of biological tissues.

PAT and Ultrasound (US) Imaging

The combination of PAT and US is a natural and widely adopted hybrid approach because both modalities share acoustic detection hardware, facilitating system integration [58] [56].

• Contrast Mechanism: US imaging provides structural information based on acoustic impedance mismatch, while PAT reveals optical absorption contrast, offering functional data such as hemoglobin concentration and oxygen saturation [58] [56].
• Applications: Integrated PA/US systems can simultaneously visualize blood vessels (via PAT) and surrounding tissue morphology (via US). This is invaluable in oncology for assessing tumor angiogenesis and hypoxia, and in visualizing sentinel lymph nodes [58] [56]. A specific implementation, transmission-reflection optoacoustic ultrasound (TROPUS), can concurrently provide images of optical absorption, acoustic reflectivity, speed of sound, and acoustic attenuation [56].

PAT and Magnetic Resonance Imaging (MRI)

Successive PAT and MRI enable co-registered hybrid-contrast imaging. While MRI offers excellent soft-tissue contrast and deep penetration, PAT provides high-resolution optical absorption information. This combination is particularly powerful for correlating functional and molecular information from PAT with detailed anatomical context from MRI [59].

PAT and Fluorescence (FL) Imaging

Combining PAT and FL imaging typically uses exogenous contrast agents to visualize complementary optical properties. The fluorescence quantum yield (Y) and the PA conversion efficiency (1-Y) are linked, allowing both signals to be detected from a single agent [58]. While FL imaging is sensitive and useful for molecular imaging, its spatial resolution degrades significantly beyond ~1 mm depth due to strong optical scattering. PAT provides higher-resolution images at greater depths, complementing the molecular information from fluorescence [58].

The workflow and information flow in a typical dual-modal PAT/US system are illustrated below.

Experimental Protocols and Methodologies

This section outlines key methodological considerations for conducting PAT experiments, from system setup to image reconstruction.

Essential System Components and Reagents

A typical PAT system requires several core components, and experiments may utilize various endogenous or exogenous contrast agents.

Table 2: The Scientist's Toolkit: Key PAT System Components and Research Reagents [55] [58]

Category	Item	Function and Key Characteristics
Core System Components	Short-Pulsed Laser	Provides nanosecond light pulses for efficient PA signal generation. Common sources: Q-switched Nd:YAG, Ti:Sapphire, OPOs. Must have tunable wavelength for spectroscopic PAT.
	Ultrasonic Transducer	Detects generated PA waves. Can be a single-element (for PAM) or an array (for PACT). Bandwidth determines axial resolution and must match PA signal frequency.
	Data Acquisition (DAQ) System	Amplifies and digitizes the detected PA signals. Requires high sampling rate (e.g., >100 MS/s) for accurate temporal signal capture.
	Synchronization Electronics	Precisely triggers the laser and DAQ to ensure signal detection is synchronized with light emission.
Contrast Agents & Reagents	Endogenous Chromophores	Natural absorbers including hemoglobin (oxygenation mapping), melanin (melanoma imaging), lipids (atherosclerosis plaque), and water [55] [56].
	Indocyanine Green (ICG)	FDA-approved exogenous contrast agent used for both PA and fluorescence imaging; applied in angiography and lymph node mapping [58].
	Methylene Blue	Contrast agent used to enhance optical absorption in specific structures, such as sentinel lymph nodes [58].
	Targeted Nanoparticles	Gold nanoparticles, carbon nanotubes, or other engineered agents functionalized to target specific molecular biomarkers (e.g., cancer cell receptors) for molecular PAT [56].

A Generalized PAT Imaging Protocol

The following workflow describes a standard procedure for a PAT experiment, such as imaging tumor vasculature in a small animal model.

• System Configuration and Calibration

  • Laser Setup: Select an appropriate wavelength based on the absorption spectrum of the target chromophore (e.g., 570 nm for deoxy-hemoglobin or 750 nm for deep penetration). Ensure pulse energy is within American National Standards Institute (ANSI) safety limits.
  • Transducer Selection: Choose a transducer with a center frequency and bandwidth suitable for the desired spatial resolution and imaging depth (e.g., a 25-MHz transducer for high-resolution shallow imaging, or a 5-MHz array for deep imaging).
  • System Synchronization: Connect the laser Q-switch output to the external trigger of the DAQ card to synchronize laser firing with data acquisition.

• Sample Preparation

  • Animal Models: Anesthetize the animal (e.g., a mouse) and securely position it on the imaging stage. Maintain body temperature using a heating pad. For longitudinal studies, use a stereotaxic frame for consistent positioning.
  • Contrast Agent Administration: If using exogenous agents (e.g., ICG), prepare a sterile solution and administer via intravenous injection (e.g., tail vein) at a specified dose (e.g., 100 µL of 100 µM ICG).

• Data Acquisition

  • Signal Detection: For PACT, fire the laser and record the PA signals from all elements of the transducer array simultaneously or in a sequential manner. For PAM, raster-scan the focused transducer assembly over the region of interest while recording the time-resolved PA signal (A-line) at each point.
  • Multi-Wavelength Acquisition: For functional or molecular imaging, acquire data sets at multiple optical wavelengths. This allows for spectroscopic analysis to separate contributions from different chromophores.

• Image Reconstruction and Processing

  • PACT Reconstruction: Apply a reconstruction algorithm (e.g., UBP, time-reversal, or a trained deep learning model) to the raw channel data from the array to form a 2D or 3D image of the initial pressure distribution ( p_0 ) [54] [57].
  • PAM Image Formation: For each A-line, apply a bandpass filter and Hilbert transform to extract the envelope-detected signal. The amplitude of this signal is used to form a 2D image for each scanning plane, which can be stacked into a 3D volume.
  • Quantitative Analysis: Use the multi-wavelength data to compute maps of total hemoglobin concentration and oxygen saturation (sOâ‚‚) based on the known absorption spectra of HbOâ‚‚ and Hb [56].

Current Research Directions and Advances

The field of PAT is continuously evolving, with several cutting-edge research directions pushing its capabilities forward.

• Artificial Intelligence and Deep Learning: AI is being leveraged to improve PAT image reconstruction, particularly from sparse or limited-view data [57]. Foundation models are also emerging; for instance, PATFOM is a universal foundation model self-supervised on nearly one million PAT images, demonstrating strong performance in multi-task image processing like restoration, segmentation, and light fluence correction [60].

• Advanced System Designs: Research focuses on developing more practical and high-performance systems. This includes all-optical PAT systems that use optical methods (e.g., holography) for non-contact acoustic detection, overcoming limitations of conventional ultrasound transducers [61]. Other efforts aim to improve deep functional imaging using techniques like virtual point sources to enhance signal fidelity [62].

• Quantitative PAT: A major challenge is accurately quantifying the concentration of chromophores, as the PA signal depends on both ( \mu_a ) and the light fluence ( F ), which is heterogeneously distributed in tissue. Advanced algorithms that model light propagation are being developed to correct for this and achieve truly quantitative images of absorption coefficients [54].

The integration of advanced biomedical optics into the drug discovery pipeline is revolutionizing two fundamental areas: the monitoring of therapy response and the delivery of targeted agents. These technologies provide researchers with the unprecedented ability to visualize biological processes in real-time, at multiple scales, and with high specificity. Framed within the basic principles of biomedical optics—which exploit the interactions between light and biological tissue—modalities such as optical imaging, optogenetics, and multimodal techniques are moving drug development beyond traditional endpoints. By enabling non-invasive, longitudinal, and quantitative assessment of drug pharmacokinetics, biodistribution, and therapeutic efficacy within living systems, these optical tools are accelerating the development of more precise and effective therapies, particularly in complex areas like oncology and neuroscience [63] [64]. This guide details the core optical technologies, experimental methodologies, and data interpretation frameworks that underpin these advanced applications.

Optical Imaging Modalities for Therapy Monitoring

A suite of optical imaging modalities is available for tracking therapy response, each with unique strengths in sensitivity, resolution, and depth penetration. The selection of an appropriate modality is critical and depends on the specific research question, the model organism, and the nature of the targeted agent.

Table 1: Key Optical Imaging Modalities in Drug Discovery

Modality	Principle	Spatial Resolution	Penetration Depth	Key Applications in Therapy Monitoring	Key Limitations
Fluorescence Imaging	Detection of light emitted by fluorescent probes (e.g., proteins, dyes) after excitation.	μm to mm	1-2 mm (Visible), several cm (NIR)	Real-time tracking of nanoparticle biodistribution [64], cell migration, and protein-protein interactions.	Limited depth penetration; scattering and autofluorescence in tissue.
Bioluminescence Imaging	Detection of light produced by luciferase enzymes in the presence of a substrate (e.g., luciferin).	mm	Several cm	Monitoring tumor growth/regression [64], gene expression, and metastatic spread in whole animals. Requires genetic modification.	Lower spatial resolution; requires substrate administration.
Fiber Photometry	Measures bulk fluorescence changes in a specific brain region via an optical fiber [65].	~100 μm (region-specific)	Several mm in brain tissue	Monitoring population-level neural activity (via Ca2+ or neurotransmitter sensors) in response to drugs or behavioral tasks [65].	Low spatial resolution; does not resolve single cells.
Miniscope (Microendoscopy)	Miniaturized microscope for direct Ca2+ imaging of neural populations in freely behaving animals [65].	μm (single-cell)	Implanted for deep brain access	Observing drug-induced plasticity and cellular adaptations underlying addiction and behavior [65].	Small field of view; invasive implantation required.

The convergence of these modalities with artificial intelligence (AI) is a key advancement. AI and machine learning algorithms enhance the interpretation of complex image datasets, improving quantification accuracy and automating workflows for more robust therapy assessment [63] [64].

Optogenetics for Circuit Dissection and Control

Optogenetics combines genetic and optical methods to achieve precise control over specific cell types or neural circuits with millisecond temporal precision [65] [66]. This tool is indispensable for establishing causal links between circuit activity and behavioral phenotypes, both in health and disease.

Core Optogenetic Tools

Optogenetic execution relies on light-sensitive proteins ("opsins") expressed in target cells. These can be ion channels for depolarization (e.g., Channelrhodopsin-2/ChR2) or ion pumps for hyperpolarization (e.g., Halorhodopsin) [65] [66]. A wide array of opsins exist with differing kinetics, spectral sensitivity, and ionic selectivity, allowing for customized experimental designs [66]. The inclusion of fluorescent proteins (FPs) as optical reporters enables simultaneous visualization of the manipulated cells [66].

Application in Addiction Research

Optogenetics has profoundly advanced the neurobiology of addiction. Key applications include:

• Circuit Mapping: By expressing channelrhodopsin in specific neurons (e.g., in the basolateral amygdala), researchers can photostimate their axon terminals in projection areas (e.g., the nucleus accumbens) to study drug-induced synaptic plasticity ex vivo [65].
• Behavioral Causality: In vivo optogenetic manipulation can directly test how defined circuits drive drug-seeking behavior. For instance, phasic stimulation of ventral tegmental area (VTA) dopamine neurons is sufficient to induce conditioned place preference and relapse-like behavior [65].

Multimodal Imaging and Hybrid Approaches

No single imaging modality possesses all desired attributes. Multimodal imaging overcomes the limitations of individual techniques by combining them, offering a more comprehensive view of drug delivery and response [64].

Table 2: Representative Hybrid Imaging Systems

Hybrid System	Combined Strengths	Application in Drug Discovery
PET/MRI	High sensitivity of PET + High soft-tissue resolution and anatomical detail of MRI.	Quantifying nanoparticle accumulation in tumors (PET) while visualizing detailed surrounding anatomy (MRI) [64].
CT/SPECT	Excellent bone/tissue visualization (CT) + Functional tracking of radiolabeled probes (SPECT).	Validating bone-targeted drug delivery systems.
Photoacoustic Imaging	High optical contrast + Ultrasonic depth penetration.	Imaging vascularization and hypoxia in tumors, monitoring responses to anti-angiogenic therapy [67].

A cornerstone of this approach is the development of multimodal imaging probes. These are single nanoparticles incorporating multiple contrast agents (e.g., a fluorophore and a radioisotope), enabling their detection across different imaging platforms [64]. For example, a receptor-targeted nanoparticle labeled with both a fluorophore and a radioisotope allows for quantitative assessment of molecular events via Positron Emission Tomography (PET) while also enabling whole-body fluorescence imaging [64].

Experimental Protocols

This section provides detailed methodologies for key experiments utilizing biomedical optics in drug discovery.

Protocol: In Vivo Tracking of Nanodrug Delivery using Multimodal Imaging

Objective: To visualize the real-time biodistribution and target engagement of a fluorescently labeled therapeutic nanoparticle.

• Nanoparticle Synthesis & Characterization:
  • Synthesize nanoparticles (e.g., liposomes, polymeric NPs) incorporating a near-infrared (NIR) fluorophore (e.g., Cy5.5, IRDye800CW) and a targeting ligand (e.g., an antibody, peptide).
  • Characterize the nanoparticles for size, surface charge, fluorophore conjugation efficiency, and targeting functionality in vitro.

• Animal Model Preparation:

  • Utilize an appropriate disease model (e.g., a mouse xenograft model of cancer).
  • For bioluminescence imaging, use tumor cells stably expressing luciferase.

• Image Acquisition:

  • Baseline Imaging: Acquire pre-injection images using all relevant modalities (e.g., MRI/CT for anatomy, fluorescence/bioluminescence for background signal).
  • NP Administration: Inject the fluorescently labeled nanoparticles intravenously.
  • Longitudinal Imaging: At multiple time points post-injection (e.g., 1, 4, 24, 48 hours), perform co-registered multimodal imaging.
    • Use Fluorescence Molecular Tomography (FMT) or 2D fluorescence imaging to track whole-body NP distribution.
    • Use MRI or CT to provide high-resolution anatomical context.
    • Use Bioluminescence Imaging to monitor tumor viability and response.

• Data Co-registration & Analysis:

  • Use software to co-register images from different modalities into a single coordinate system.
  • Quantify fluorescence signal intensity in the tumor region of interest (ROI) over time to generate a biodistribution profile.
  • Correlate the NP accumulation (fluorescence) with therapeutic response (change in bioluminescence signal).

Protocol: Monitoring Neural Circuit Response to Therapy using Fiber Photometry

Objective: To record population-level neural activity in a specific brain circuit during drug administration and subsequent behavior.

• Virus Injection:
  • Stereotactically inject a virus (e.g., AAV) encoding a genetically encoded calcium indicator (GECI, e.g., GCaMP) into the brain region of interest (e.g., Nucleus Accumbens, NAc) of an animal.

• Optical Fiber Implantation:

  • Immediately following the virus injection, implant an optical fiber cannula directly above the infected region to allow for light delivery and collection.

• Habituation & Setup:

  • After a several-week period for viral expression and recovery, habituate the animal to the experimental setup and tethering to the photometry system.

• Recording Session:

  • Deliver the excitation light (e.g., ~465 nm for GCaMP) and collect the emitted fluorescence signal through the implanted fiber.
  • Simultaneously, record a reference signal (e.g., ~405 nm isosbestic point) to control for motion artifacts and autofluorescence.
  • Administer the drug or vehicle control while recording the fluorescence signal.
  • The animal can also be engaged in a behavioral task (e.g., a lever-pressing task) to correlate neural activity with behavior.

• Data Processing:

  • Calculate the relative change in fluorescence (ΔF/F) from the 465 nm signal, normalized using the 405 nm reference.
  • Align the processed photometry data with the timestamps of drug administration or behavioral events to identify activity patterns correlated with the treatment.

Visualization of Signaling Pathways and Workflows

The following diagrams, created using DOT language and adhering to the specified color palette and contrast rules, illustrate key concepts and workflows.

Neural Circuit Mapping with Optogenetics

This diagram illustrates the experimental workflow for using optogenetics to map and characterize neural circuits involved in drug response, revealing sites of drug-induced plasticity.

Multimodal Imaging for Therapy Assessment

This diagram outlines the integrated workflow for using co-registered multimodal imaging to track targeted nanodrugs and quantify therapy response in real-time.

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Essential Research Reagents and Materials

Item	Function/Description	Example Application
Genetically Encoded Calcium Indicators (GECIs)	Fluorescent proteins (e.g., GCaMP) that increase brightness upon binding Ca2+, serving as a proxy for neural activity.	Monitoring population-level neural activity in response to a drug using fiber photometry or miniscopes [65].
Channelrhodopsin-2 (ChR2)	A light-gated cation channel that depolarizes and excites neurons upon blue light stimulation.	Causally testing the role of a specific neural pathway in drug-seeking behavior [65] [66].
Targeted Fluorescent Nanoparticles	Drug carriers (liposomes, polymeric NPs) conjugated with a fluorophore and a targeting ligand (e.g., antibody, peptide).	Visualizing the real-time biodistribution and tumor accumulation of a nanodrug [64].
Luciferase Reporters	Enzymes (e.g., firefly luciferase) that produce light in the presence of a substrate (luciferin).	Monitoring tumor burden or therapeutic efficacy longitudinally in vivo via bioluminescence imaging [64].
AlphaFold	AI-driven algorithm that predicts the 3D structure of proteins from their amino acid sequence.	Accelerating target identification and drug design by revealing potential binding sites for novel therapeutics [63].
PandaOmics	An AI-powered platform that integrates multi-omics data and text mining to identify and rank novel drug targets.	Systematically prioritizing new, druggable genes for ocular and neurological diseases [63].
GK921	GK921, MF:C21H20N4O, MW:344.4 g/mol	Chemical Reagent
Pralidoxime	Pralidoxime, CAS:51-15-0; 94-63-3, MF:C7H9N2O+, MW:137.16 g/mol	Chemical Reagent

Optimizing Performance and Overcoming Challenges in Optical Device Design

In biomedical optics research, from the development of novel imaging devices to advanced drug delivery systems, the packaging is far more than a simple container; it is the critical interface that ensures a product's safety, efficacy, and reliability. For researchers and scientists, navigating the stringent requirements of medical compliance, material science, and packaging design is a fundamental multidisciplinary challenge. A failure in packaging can compromise the most innovative optical sensor or therapeutic agent, rendering years of research futile. This guide provides an in-depth examination of the core design principles governing this essential field, framing them within the rigorous context of biomedical research and development. It aims to equip professionals with the knowledge to design packaging systems that not only meet global regulatory standards but also preserve the integrity of sensitive biomedical products from the laboratory to the end-user.

Medical Compliance and Regulatory Frameworks

Adherence to international standards and regulations is the non-negotiable foundation of medical device packaging. These frameworks ensure that packaging systems reliably protect product sterility and performance, thereby safeguarding patient safety.

Key Global Standards and Regulations

• ISO 11607-1 and -2: This is the paramount standard for terminally sterilized medical devices. Part 1 specifies the requirements for materials, sterile barrier systems, and packaging design, mandating that materials are non-toxic, free of defects, and manufactured from known, traceable sources [68] [69]. Part 2 outlines the validation requirements for the forming, sealing, and assembly processes, establishing a quality framework similar to that used for the devices themselves [68] [69].
• U.S. FDA 21 CFR Part 820: The U.S. Food and Drug Administration's Quality System Regulation treats packaging as an integral part of the medical device. Section 820.160 details best practices for device manufacturers, including packaging processes, and applies equally to third-party packaging manufacturers [68] [70].
• European Union Medical Device Regulation (EU MDR): Regulation (EU) 2017/745 establishes requirements for the EU market, focusing on patient safety and the suitability of packaging design for sterile devices [68].
• Other Standards: The International Safe Transit Association (ISTA) and ASTM-D4169 standards provide testing procedures to validate that packaging can withstand the physical stresses of distribution and transportation [69].

The Validation Lifecycle: IQ, OQ, and PQ

Regulatory compliance is demonstrated through a rigorous validation lifecycle. This process provides documented evidence that packaging systems are consistently produced and perform as intended [70].

• Installation Qualification (IQ): Verifies that packaging equipment is correctly installed according to approved specifications.
• Operational Qualification (OQ): Demonstrates that the equipment operates consistently within defined parameters under all anticipated operating conditions.
• Performance Qualification (PQ): Confirms that the final packaging process, under routine production conditions, consistently produces packages that meet all predefined quality and performance criteria.

Table 1: Key International Standards for Medical Device Packaging

Standard / Regulation	Jurisdiction / Body	Primary Focus	Key Requirements
ISO 11607-1	International (ISO)	Materials & Design	Materials must be non-toxic, traceable, and defect-free; defines sterile barrier system requirements [69].
ISO 11607-2	International (ISO)	Process Validation	Validation of forming, sealing, and assembly processes [69].
21 CFR Part 820	United States (FDA)	Quality System	Packaging is considered part of the device; defines manufacturing practices and labeling [68] [70].
EU MDR	European Union	Safety & Performance	Requirements for packaging design and suitability to ensure device safety [68].
ISTA/ASTM-D4169	International	Transportation Testing	Simulates vibration, shock, and other distribution hazards [69].

Diagram 1: Packaging Validation Workflow

Material Selection for Medical Device Packaging

The selection of packaging materials is a critical decision that controls every subsequent aspect of the packaging system. It requires a balance between barrier properties, compatibility with sterilization, and mechanical performance.

Material Types and Properties

Materials are chosen based on the specific needs of the device, particularly its sensitivity to environmental factors like moisture and oxygen.

• High-Impact Polystyrene (HIPS): A common, cost-effective material for rigid trays. It is lightweight, durable, and easily formable. Recycled HIPS is often used as an environmentally friendly option [68].
• Polyethylene Terephthalate (PET & RPET): Offers good durability and clarity. Recycled PET (RPET) is a sustainable choice, and RPET ESD (electrostatic dissipative) variants are available to protect sensitive electronic medical devices [68].
• Polyethylene Glycol (PEG): A synthetic polymer approved by the FDA for ophthalmic and other uses. It is hydrophilic, biocompatible, and used in controlled-release drug delivery implants, such as the Dextenza intracanalicular insert [71].
• Poly(lactic-co-glycolic acid) (PLGA): A biodegradable synthetic polymer that is FDA-approved for ocular applications. Its degradation rate can be tuned to control drug release kinetics, making it highly valuable for sustained-release formulations [71].
• High-Barrier Films: These are multilayer structures often incorporating materials like ethylene vinyl alcohol (EVOH) or polyvinylidene chloride (PVDC) as core barrier layers to block gases and moisture. These are laminated to substrates like polyester or polypropylene for mechanical strength [72].

Critical Material Properties and Testing

• Barrier Performance: The primary function of many packaging systems is to prevent the ingress of moisture and oxygen, which can degrade sensitive products. This is quantified by the Water Vapor Transmission Rate (WVTR) and Oxygen Transmission Rate (OTR) [73] [72].
• Sterilization Compatibility: Materials must withstand the chosen sterilization method (e.g., gamma radiation, ethylene oxide, steam autoclave) without degrading, becoming brittle, or releasing harmful compounds [70].
• Shelf-Life and Accelerated Aging: Materials must maintain their integrity and barrier properties throughout the product's intended shelf life. Accelerated aging studies are conducted by exposing packaged products to elevated temperatures to model long-term stability in a shorter time frame [68] [69].

Table 2: Common Materials for Medical Device Packaging

Material	Material Type	Key Properties	Common Applications
HIPS (Recycled)	Plastic Polymer	Lightweight, durable, formable, cost-effective [68].	Molded trays for instruments and implants.
RPET & RPET ESD	Plastic Polymer	Durable, sustainable; ESD version protects electronics [68].	Trays and blisters for devices with sensitive components.
PEG	Synthetic Polymer	Hydrophilic, biocompatible, tunable erosion rate [71].	Drug-delivery implants (e.g., Dextenza).
PLGA	Biodegradable Polymer	Biocompatible, tunable degradation and drug release [71].	Sustained-release drug delivery systems.
EVOH	High-Barrier Polymer	Excellent gas barrier properties [72].	Layer in multilayer films for sensitive pharmaceuticals.

Packaging Design, Testing, and Integration

A successful packaging design integrates the selected materials into a robust system that survives the supply chain and remains easy for the end-user to open without compromising sterility.

Integrity and Seal Strength Testing

Package integrity is paramount for sterile devices. Testing goes beyond visual inspection to detect microscopic failures.

• Dye Penetration Test: A dye solution is applied to the package seals; penetration indicates a leak path [69] [70].
• Bubble Emission Test: The sealed package is submerged underwater and placed in a vacuum chamber; escaping air forms bubbles, revealing leaks [69].
• Vacuum Decay Test: An automated, non-destructive method that detects pressure changes in a test chamber caused by leaks in the package [70].

Distribution Testing

Packaging must protect the device through the physical hazards of shipping. The ISTA standards provide predefined test sequences that simulate vibrations, shocks, compression forces, and atmospheric conditions encountered in distribution environments [69] [70].

Experimental Protocol: Package Integrity Validation

This protocol outlines a standard approach for validating the integrity of a sterile barrier system, such as a sealed pouch or tray.

• Objective: To demonstrate that the sealed packaging maintains a complete microbial barrier under defined test conditions.
• Materials & Equipment:
  • Sealed sterile barrier packages (test samples).
  • Negative control (unsealed or intentionally compromised package).
  • Dye penetration test kit (e.g., methylene blue solution).
  • Vacuum chamber and pressure gauge.
  • Inspection fixtures.
• Methodology:
  • Sample Preparation: Place the test sample and negative control in the dye solution, ensuring the seal areas are fully wetted.
  • Application of Vacuum: Subject the chamber to a defined vacuum level (e.g., 0.3-0.5 bar) for a specified dwell time (e.g., 30 seconds).
  • Release and Inspection: Slowly release the vacuum. Rinse the exterior of the packages and carefully inspect the seal areas for any trace of dye penetration under appropriate lighting.
  • Analysis: The test is a pass if no dye penetration is observed in the test samples. The negative control must show penetration to confirm the test was valid.
• Documentation: Record the vacuum level, dwell time, number of samples tested, and results for each sample. This data forms a critical part of the validation report [69] [70].

Diagram 2: Integrity Test Workflow

The Scientist's Toolkit: Research Reagent Solutions

For researchers developing and testing new packaging systems or drug-delivery implants, a specific set of materials and reagents is essential.

Table 3: Essential Research Reagents and Materials

Item	Function/Description	Application Example
PLGA (various ratios)	A copolymer whose degradation rate is controlled by the lactic to glycolic acid ratio; enables tunable drug release profiles [71].	Fabricating microspheres for sustained release of ophthalmic drugs.
PEG-based Hydrogels	Biocompatible, water-swollen networks used as drug reservoirs or in-situ forming implants for controlled release [71] [74].	Developing intracanalicular inserts (e.g., Dextenza) or injectable depots.
EVOH Resin	A high-barrier polymer used in the research and development of multilayer film structures to protect sensitive products from oxygen degradation [72].	Creating prototype high-barrier pouches for oxygen-sensitive diagnostics.
Dye Penetration Test Kit	A quality control reagent used to visually identify microscopic channels or defects in package seals [69] [70].	Validating the seal integrity of a new pouch design.
Accelerated Aging Chambers	Environmental chambers that simulate long-term shelf life by exposing packaged products to controlled, elevated temperatures [68] [69].	Determining the probable shelf-life of a new device-packaging system.
Aspulvinone O	Aspulvinone O, MF:C27H28O6, MW:448.5 g/mol	Chemical Reagent

The field of medical packaging is dynamically evolving, driven by technological innovation and shifting market demands. Key future trends include:

• Smart Packaging: The integration of RFID tags, temperature indicators, and digital authentication features enables real-time supply chain tracking, ensures cold-chain maintenance, and combats counterfeiting [72] [70].
• Advanced Drug Delivery Systems: Innovations in nanotechnology, microfluidics, and biodegradable polymers are creating new paradigms for drug delivery, such as implantable microfluidic systems for targeted therapy and wearable patches for continuous monitoring [75] [74].
• Sustainability: There is a growing focus on developing sustainable solutions, including the use of bio-based polymers, recycled materials (like rHIPS and rPET), and reduced-packaging designs that maintain strict performance and sterility requirements [68] [73] [70].

In conclusion, the design of medical device packaging is a sophisticated discipline that sits at the intersection of material science, regulatory law, and engineering. For researchers and scientists in biomedical optics and drug development, a deep understanding of compliance, material properties, and rigorous testing protocols is not merely a regulatory hurdle—it is a fundamental component of translational success. By integrating these critical design considerations from the earliest stages of product development, innovators can ensure their advanced technologies are delivered safely and effectively, ultimately protecting patient health and upholding the highest standards of scientific integrity.

• Introduction to tolerance analysis: Importance in biomedical optics system design.
• Core principles: Fundamental concepts and performance criteria with quantitative examples.
• Methodological framework: Step-by-step experimental protocols for tolerance analysis.
• Case study: Application in laser diode collimation system with performance data.
• Implementation strategies: Alignment techniques and tolerance budgeting workflow.
• Research toolkit: Essential materials and reagents for experimental research.

---

The Critical Role of Comprehensive Tolerance Analysis in System Performance

Tolerance analysis represents a systematic methodology for evaluating how variations in component manufacturing, assembly, and alignment affect overall system performance. In biomedical optics, where systems increasingly incorporate miniaturized components and must operate under demanding conditions, comprehensive tolerance analysis transitions from an engineering best practice to an essential requirement. The development of advanced biomedical imaging systems—including confocal microscopes, flow cytometers, optical coherence tomography (OCT) systems, and endoscopic imaging devices—demands rigorous tolerance analysis throughout the design process. These systems typically integrate multiple optical elements (lenses, mirrors, filters), light sources (lasers, LEDs), detection systems, and increasingly, micro-optical components that require precise alignment to function optimally [76].

The fundamental challenge addressed by tolerance analysis is the inherent variability introduced during manufacturing and assembly processes. Even with advanced manufacturing techniques, dimensional variations inevitably occur and can propagate through optical paths, resulting in degraded image quality, reduced signal-to-noise ratios, or complete system failure. In biomedical applications, these performance degradations can directly impact diagnostic accuracy or research outcomes. Tolerance analysis provides a quantitative framework for establishing acceptable variation limits while maintaining required performance levels, thereby enabling designers to balance performance requirements with manufacturability and cost constraints [76].

Core Principles of Tolerance Analysis

Fundamental Concepts and Terminology

Tolerance analysis in optical systems operates on several foundational concepts that enable engineers to predict system performance under real-world manufacturing conditions. Alignment sensitivity refers to how significantly system performance changes in response to misalignments of individual components. Parameters commonly analyzed include decentering (lateral displacement), tilt (angular misalignment), despace (longitudinal positioning error), and rotation about the optical axis. Each degree of freedom presents unique challenges for system assembly and performance stability. The most critical insight from comprehensive tolerance analysis is that certain misalignments often demonstrate dramatically higher sensitivity than others, necessitating prioritized control during manufacturing [76].

Performance criteria must be carefully selected to represent system functionality accurately. In biomedical optics, these typically include throughput efficiency (critical for low-light applications like fluorescence microscopy), beam homogeneity (essential for quantitative imaging), wavefront error (determining spatial resolution), and angular beam properties (defining field of view and spatial coverage). These metrics must be derived from overarching system requirements, such as the minimum detectable contrast in medical imaging or spatial resolution required for cellular imaging. The relationship between misalignments and these performance criteria is often complex and non-linear, requiring sophisticated modeling approaches to understand fully [76].

Performance Requirements and Specification

Establishing clear, quantifiable performance requirements represents the essential first step in tolerance analysis. These requirements should be traceable to the biomedical application's fundamental needs. For example, a flow cytometer's optical system must maintain specific illumination uniformity across the sample stream and collection efficiency from emitted fluorescence to ensure consistent cell population discrimination. Similarly, an OCT system requires precise wavefront quality to achieve the axial resolution necessary for distinguishing tissue layers [76].

Table 1: Performance Criteria for Optical Systems in Biomedical Applications

Performance Criterion	Impact on Biomedical System	Measurement Approach
Throughput Efficiency	Signal-to-noise ratio in low-light imaging	Minimum transmission within defined angular window
Beam Homogeneity	Quantitative measurement accuracy	Intensity variation across beam profile
Wavefront Error	Spatial resolution and image contrast	RMS wavefront error relative to ideal
Angular Beam Properties	Field of view and spatial coverage	Divergence angles in fast and slow axes
Strehl Ratio	Overall image quality	Ratio of actual to theoretical peak intensity

Requirements should include both performance thresholds (minimum acceptable values) and goal values (desired performance levels). For instance, a confocal microscope might require a minimum of 70% throughput efficiency but aim for 85% in the design. These specifications directly determine the tolerances that can be permitted—tighter performance requirements typically necessitate stricter tolerances and consequently higher manufacturing costs [76].

Methodological Framework for Tolerance Analysis

Experimental Protocol for Comprehensive Tolerance Analysis

Implementing a structured approach to tolerance analysis ensures consistent results and traceable decisions. The following protocol provides a systematic methodology applicable to diverse biomedical optical systems:

• Requirements Definition: Document all system performance requirements derived from biomedical application needs. Convert clinical or research requirements (e.g., "must resolve cellular structures ≤2μm") into specific optical performance parameters (e.g., modulation transfer function at 500 lp/mm). Establish minimum acceptable values and goal values for each parameter [76].

• Optical Modeling: Create a parameterized computer model of the optical system using specialized software (e.g., Zemax, Code V, or FRED). The model should include all optical elements with their nominal positions and orientations. Verify model accuracy by comparing performance predictions with theoretical calculations for the nominal design [76].

• Sensitivity Analysis: Introduce small, controlled perturbations to each degree of freedom for each optical component while holding other parameters at nominal values. Common perturbations include:

  • Lateral decentering: ±1-10μm
  • Axial displacement: ±5-50μm
  • Tilt: ±0.1-1.0°
  • Rotation: ±0.5-2.0° Quantify the sensitivity coefficient for each parameter as the change in performance metrics per unit change in the parameter [76].

• Monte Carlo Analysis: Randomly vary all parameters simultaneously according to their expected statistical distributions (typically normal or uniform distributions). Execute hundreds or thousands of trials to simulate manufacturing outcomes. Record performance metrics for each trial to build a statistical distribution of expected system performance [76].

• Tolerance Allocation: Based on sensitivity and Monte Carlo analysis results, assign specific tolerance values to each parameter. Focus on controlling the most sensitive parameters while permitting looser tolerances on insensitive parameters. Validate that the allocated tolerances yield acceptable yield rates (typically >90% for commercial systems) [76].

• Alignment Procedure Development: Design alignment procedures that efficiently control the most sensitive parameters. Determine whether passive alignment (using mechanical references), active alignment (using performance feedback), or hybrid approaches provide the optimal balance of precision, speed, and cost [76].

Quantitative Analysis and Performance Prediction

The mathematical foundation of tolerance analysis relies on establishing the relationship between parameter variations and system performance. For complex optical systems, this typically involves ray tracing simulations that model light propagation through the perturbed system. The resulting performance data enables statistical prediction of manufacturing yields and identification of performance-limiting components [76].

Table 2: Exemplary Tolerance Sensitivity Data for a Micro-Optical Collimation System

Parameter	Misalignment Range	Performance Impact	Sensitivity Classification
Acylinder Rotation	±0.5°	Throughput reduction: 15-40%	Highest sensitivity
Lens Decenter	±2μm	Wavefront error increase: 0.05-0.12λ RMS	Medium sensitivity
Lens Tilt	±0.3°	Angular deviation: 0.02-0.08°	Medium sensitivity
Axial Spacing	±10μm	Throughput reduction: 2-8%	Lower sensitivity
Source Position	±5μm	Beam homogeneity change: 3-12%	Component-dependent

The experimental workflow for tolerance analysis follows a logical progression from system definition through to alignment specification, with iterative refinement between steps:

Diagram 1: Tolerance Analysis Workflow (55 characters)

Case Study: Tolerance Analysis in Laser Diode Array Collimation

A detailed case study from laser diode array collimation for LiDAR systems provides valuable insights applicable to biomedical optics, particularly for illumination systems in advanced microscopes or flow cytometers. The system employed a laser diode array source, a microlens array for slow-axis collimation, and an acylinder for fast-axis collimation. The optical system featured an overall footprint in the millimeter range with micrometer-sized features, presenting significant alignment challenges [76].

The performance requirements for this system included stringent throughput efficiency targets (65% overall optical efficiency) and precise angular beam properties derived from the need to detect and resolve objects measuring 13.1 × 12.0 cm² at distances up to 80 meters. These application requirements translated into specific optical performance criteria, including a minimum throughput of 4.375% per segment within a defined angular window (±3.75° horizontal, ±0.086° vertical) and a beam height requirement that more than 86.5% (1/e² boundary) of the beam's vertical energy must remain within ±0.086° [76].

Tolerance Analysis Results and Critical Findings

The tolerance analysis revealed that acylinder rotation around the optical axis represented the most sensitive parameter, with misalignments of just ±0.5° causing throughput reductions of 15-40%. This finding significantly influenced the alignment strategy, necessitating active alignment for this specific degree of freedom. Other parameters, such as lens decenter and tilt, showed medium sensitivity, while axial spacing variations demonstrated relatively lower impact on system performance [76].

The relationship between specific misalignments and optical performance followed complex, often non-linear patterns that would have been difficult to predict without comprehensive modeling. For instance, certain combinations of misalignments produced compensatory effects, while others resulted in performance degradation greater than the sum of individual effects. The tolerance analysis enabled the development of a prioritized alignment procedure that focused effort on controlling the most critical parameters while verifying the alignment of less sensitive parameters [76].

Table 3: Impact of Misalignments on Optical Performance Metrics

Misalignment Type	Throughput Reduction	Beam Profile Degradation	Alignment Method Recommended
Acylinder Rotation	15-40%	Significant asymmetry	Active alignment
Lens Decenter	5-15%	Moderate asymmetry	Passive alignment with precision fixtures
Lens Tilt	8-20%	Beam steering and shape distortion	Hybrid alignment
Axial Spacing	2-8%	Minimal shape change	Passive alignment
Source Position	5-18%	Dependent on specific configuration	Active alignment

Implementation Strategies for Biomedical Optical Systems

Alignment Techniques and Methodologies

The tolerance analysis results directly inform the selection of appropriate alignment methodologies. Passive alignment techniques rely on precision mechanical fixtures and manufacturing to position components correctly without performance feedback. This approach offers advantages in speed, cost, and scalability but provides limited flexibility for compensating manufacturing variations. Active alignment utilizes real-time performance feedback to optimize component position, offering higher potential precision at the cost of increased complexity, time, and expense [76].

Based on tolerance sensitivity findings, optical systems typically employ hybrid alignment strategies that combine passive and active techniques according to parameter criticality. The highest sensitivity parameters warrant active alignment, while medium and lower sensitivity parameters can often be adequately controlled through passive methods. The alignment concept should be developed concurrently with the optical design rather than as an afterthought, as design modifications can sometimes dramatically reduce alignment sensitivity [76].

Tolerance Budgeting and Yield Optimization

The process of tolerance budgeting translates sensitivity analysis results into manufacturable specifications. This involves assigning specific tolerance values to each parameter to achieve an acceptable yield at reasonable cost. The fundamental principle is to allocate tighter tolerances to high-sensitivity parameters and looser tolerances to low-sensitivity parameters. Statistical analysis using methods like Monte Carlo simulation predicts the expected system performance distribution and manufacturing yield [76].

The following diagram illustrates the decision process for selecting alignment methods based on tolerance analysis results:

Diagram 2: Alignment Strategy Selection (53 characters)

The Scientist's Toolkit: Research Reagent Solutions

Implementing comprehensive tolerance analysis requires both computational tools and physical measurement systems. The following essential resources enable rigorous evaluation of optical system tolerances:

Table 4: Essential Research Tools for Tolerance Analysis in Biomedical Optics

Tool Category	Specific Examples	Function in Tolerance Analysis
Optical Simulation Software	Zemax, Code V, FRED, ASAP	Models system performance with parameter variations
Ray Tracing Tools	Custom MATLAB/Python scripts, OpticStudio	Simulates light propagation through misaligned systems
Metrology Instruments	Interferometers, autocollimators, wavefront sensors	Measures actual component and system performance
Precision Alignment Equipment	Multi-axis stages, micro-manipulators, active alignment stations	Implements alignment strategies with required precision
Statistical Analysis Packages	JMP, Minitab, custom statistical scripts	Analyzes sensitivity data and predicts manufacturing yield

These tools collectively enable the implementation of the complete tolerance analysis workflow, from initial modeling through final validation. The selection of specific tools should be guided by the system complexity, performance requirements, and available resources [76].

Comprehensive tolerance analysis provides an indispensable framework for developing robust, high-performance optical systems for biomedical applications. By systematically evaluating how variations affect system performance, designers can identify critical parameters, allocate appropriate tolerances, and develop efficient alignment strategies. The methodology demonstrated in the laser diode collimation case study—including sensitivity analysis, Monte Carlo simulation, and prioritized alignment—translates directly to biomedical optical systems ranging from diagnostic instruments to research microscopes. As biomedical optics continues to advance toward miniaturized systems with increasingly demanding performance requirements, tolerance analysis will play an ever more critical role in bridging design aspirations to manufacturable realities.

Strategies for Scatter Management and Enhancing Signal-to-Noise in Turbid Media

In biomedical optics research, a turbid medium is a material where light is simultaneously absorbed and scattered, a description that applies to most biological tissues. The fundamental challenge when working with such media is that scattering overwhelms the desired signal, leading to degraded image contrast, reduced penetration depth, and diminished quantitative accuracy in spectroscopic measurements. Effectively managing this scattered light is therefore paramount for techniques ranging from deep-tissue imaging to non-invasive biosensing. This guide synthesizes core principles and advanced strategies for controlling scattering and enhancing the signal-to-noise ratio (SNR), which form the foundation for extracting meaningful biological data from optical systems.

The interaction of light with turbid media is primarily characterized by two phenomena: absorption, which converts light energy to other forms (e.g., heat), and scattering, which redirects the path of photons. The competition between these processes defines the light's behavior within the medium. Scattering can be further described by the reduced scattering coefficient (μs), which represents the effective scattering after accounting for the anisotropy of scattering events. The combined effect of absorption and scattering is quantified by the effective attenuation coefficient (μeff), given by μeff = √(3μa(μa + μs)) [77]. Mastering the separation and quantification of these properties is the first step in scatter management.

Core Technical Approaches and Their Quantitative Performance

Several strategic approaches have been developed to isolate the desired "ballistic" photons (which travel straight without scattering) from the unwanted scattered photons. These methods leverage differences in physical properties such as time-of-flight, polarization state, spatial structure, and angular distribution.

The table below summarizes the key scatter-management techniques, their underlying principles, and their reported performance metrics.

Table 1: Comparison of Core Scatter-Management Techniques in Turbid Media

Technique	Fundamental Principle	Key Performance Metrics	Reported Performance
Time-Gated Imaging [78]	Temporally gates the detector to accept only early-arriving photons (ballistic and snake), rejecting late-arriving scattered photons.	Signal-to-Noise Ratio (SNR), Image Contrast	Outperforms conventional imaging in both SNR and target contrast [78].
Polarization-Difference Imaging [78]	Exploits depolarization of scattered light vs. preserved polarization of surface-reflected light; uses cross-polarization to suppress scattered light.	Degree of Polarization (DoP), Contrast-to-Noise Ratio	Effectively suppresses residual backscattered light within a gated slice, enhancing contrast [78].
Spatially Modulated Spectroscopy (SMoQS) [79]	Projects structured illumination patterns; analyzes the modulation transfer function to decouple absorption (μa) from reduced scattering (μs) coefficients.	R² of recovered vs. known optical properties	Phantom validation: R² = 0.985 for μa, R² = 0.996 for μs across 430-1050 nm [79].
Computational Ghost Imaging (CGI) [80]	Uses single-pixel detection and structured illumination patterns; correlates patterns with bucket detector signals to reconstruct an image, proving resilient to scattering noise.	Signal-to-Noise Ratio (SNR) of reconstructed image	A novel method using statistical averaging and deconvolution successfully reconstructs images of objects hidden in dynamic turbid media [80].
Angularly-Resolved Radiance [77]	Measures angular distribution of light exiting a medium; uses diffusion theory ratios to extract μeff and diffusion coefficient (D) from relative radiance measurements.	Accuracy of extracted μa and μs	Validated for extracting μeff(λ) and D(λ) from Intralipid-1% in the 450-950 nm range [77].

Hybrid and Emerging Approaches

The integration of multiple physical principles into hybrid systems often yields superior performance. For instance, Polarization-Difference Range-Gated Imaging (p-RGI) combines temporal and polarization filtering. The range-gating mechanism first performs a primary suppression of backscattering noise, after which the polarization-difference processing eliminates the residual backscattered light that persists within the temporal gate [78]. This dual-mechanism approach has been demonstrated to outperform conventional imaging methods in turbid media.

Emerging trends also point to the growing influence of machine learning in combating scattering. AI-driven design is being used to rapidly discover and optimize nanophotonic structures for specific optical responses, enabling new paths for controlling light in complex media [81]. Furthermore, computational techniques like non-blind deconvolution are being paired with physical methods like CGI to further refine reconstructed images by matching a Gaussian kernel to the point spread function of the imaging system, thereby enhancing final SNR [80].

Detailed Experimental Protocols

To ensure reproducibility and provide a practical toolkit for researchers, this section outlines detailed methodologies for two key techniques: Spatially Modulated Quantitative Spectroscopy and Polarization-Difference Range-Gated Imaging.

Protocol: Spatially Modulated Quantitative Spectroscopy (SMoQS)

SMoQS is a non-contact method for quantifying the absolute absorption and reduced scattering coefficients of a turbid sample across a broad spectral range (430-1050 nm) without a priori assumptions of its composition [79].

Table 2: Research Reagent Solutions for SMoQS Phantom Validation

Item	Function / Rationale
Intralipid (20%)	A well-characterized, standardized source of lipid scatterers used to create tissue-simulating liquid phantoms with predictable scattering properties [79].
Nigrosin	A broadband absorbing dye with a spectral profile that mimics tissue (strong in visible, weak in NIR), allowing a large dynamic range of absorption values in a single phantom [79].
Spectrophotometer	Used for independent, quantitative confirmation of the absorption spectrum and concentration of the nigrosin stock solution without scatterers present [79].
Liquid Reference Phantom	A phantom with precisely known optical properties (e.g., μa, μs) is essential for calibrating the system and characterizing the instrument's inherent modulation transfer function (MTF) [79].

Procedure:

• Instrument Setup: Configure a system consisting of a broadband tungsten-halogen lamp, a digital micromirror device (DMD) for pattern projection, and a spectrally-resolved detector (spectrometer with a cooled CCD) [79].
• Illumination Pattern Projection: Project a series of 15 two-dimensional sinusoidal illumination patterns onto the sample surface. The spatial frequency (f_x) of these patterns should range from 0 to 0.2 mm⁻¹ in increments of 0.05 mm⁻¹ [79].
• Phase-Shifted Acquisition: For each spatial frequency, project the pattern three times with phase shifts of 0°, 120°, and 240°. Collect the remitted light from a 2-mm diameter subsection within the illuminated region for each phase [79].
• Reference Measurement: Perform an identical measurement sequence on a calibration phantom with known optical properties.
• Data Demodulation: For each wavelength, calculate the AC component of the reflectance (M_AC) using the formula: M_AC(λ, f_x) = (2/3) * √( [I₁(λ,f_x) - I₂(λ,f_x)]² + [I₂(λ,f_x) - I₃(λ,f_x)]² + [I₃(λ,f_x) - I₁(λ,f_x)]² ) where I_i denotes the measured reflectance spectrum at each of the three projected phases [79].
• Calibration: Use the demodulated data from the reference phantom to convert the sample's AC reflectance into absolute units.
• Inverse Model Fitting: At each wavelength, fit the measured MTF (the decay of M_AC as a function of spatial frequency) to a Monte Carlo-based light transport model. This fitting process independently recovers the absorption coefficient (μa) and the reduced scattering coefficient (μs) across the entire spectrum [79].

Protocol: Polarization-Difference Range-Gated Imaging (p-RGI)

This hybrid method is designed for active imaging in turbid environments, such as underwater, combining temporal and polarization gating for enhanced target contrast [78].

Procedure:

• System Synchronization: Coordinate a pulsed laser and a gated camera with a synchronization controller. The laser emits a short pulse of polarized light with pulse width T_p [78].
• Timing Configuration: Set the camera's gate delay T_1 to be equal to the round-trip time of light to the target (T_0 = 2d/c, where d is target distance and c is the speed of light in the medium). Set the camera's exposure duration T_s to be equal to T_p. This ensures the gate opens precisely when the target-reflected light arrives and collects the entire signal while excluding most backscattered light [78].
• Image Acquisition:
  • Acquire a sequence of range-gated images.
  • For polarization analysis, acquire images at multiple (e.g., four) polarization orientations of the analyzer (e.g., 0°, 45°, 90°, 135°) [78].
• Polarization-Difference Processing: Calculate the Stokes vector components from the images at different polarization angles. Use these components to compute a polarization-difference image that emphasizes light whose polarization state has been preserved (e.g., target reflection) and suppresses depolarized backscattered light [78].
• Image Fusion: Fuse the multiple gated images and polarization parameters to achieve a final image with a high SNR [78].

Visualization of Core Concepts and Workflows

The following diagrams illustrate the logical relationships and workflows for the key techniques discussed in this guide.

Diagram 1: p-RGI Process Flow

Diagram 2: SMoQS Logical Flow

The advancement of biomedical optics research is fundamentally reliant on the precision and reliability of its optical systems. Validation and testing protocols, spanning from component-level Modulation Transfer Function (MTF) to system-level wavefront error analysis, provide the critical framework for ensuring that these systems meet the stringent requirements necessary for scientific discovery and clinical application. These processes are not merely procedural checkpoints but are integral to the entire device life cycle, from initial proof-of-principle and design optimization to clinical trial standardization and post-market surveillance [82]. In the context of biomedical optics, where technologies are increasingly deployed for sensitive applications such as disease diagnosis, neural imaging, and surgical guidance, rigorous validation is the cornerstone of technological maturity and successful clinical translation.

The basic principles governing this validation paradigm require a holistic approach that considers both individual component performance and integrated system behavior. As optical systems in biomedicine become more sophisticated—incorporating complex computational imaging, multi-modal approaches, and miniaturized designs—the protocols for verifying their performance must similarly evolve. This guide establishes a comprehensive technical framework for these validation protocols, emphasizing their critical role within the broader thesis of biomedical optics research: that reliable optical data is foundational to biological insight and medical progress. By adhering to standardized, phantom-based test methods that can be incorporated into international consensus standards, researchers can directly facilitate the clinical translation and commercial success of biomedical optical technologies [82].

Theoretical Foundations of Optical Performance Metrics

Modulation Transfer Function (MTF) and Contrast Transfer

The Modulation Transfer Function (MTF) is a fundamental metric for quantifying the spatial resolution and contrast performance of an optical component or system. It describes the ability of an optical system to transfer contrast from the object to the image at various spatial frequencies, typically expressed as a function ranging from 0 (no contrast transfer) to 1 (perfect contrast transfer) [83]. In practical terms, MTF characterizes how well a system can resolve fine details, with higher MTF values at higher spatial frequencies indicating superior resolution capability.

In biomedical optics, the MTF is particularly crucial for imaging applications where discerning minute biological structures is essential. However, the standardized MTF has limitations; it is strictly exact only for objects with sinusoidal intensity distribution and assumes continuous energy spread. Real-world biological objects are finite, often resulting in better actual contrast transfer and resolution than the MTF would indicate [83]. The combined effect of multiple optical components on MTF is not arithmetic. For relatively small, unrelated wavefront errors, the combined MTF can be approximated as the product of individual MTF values, meaning the combined contrast transfer at every spatial frequency is the product of the individual component transfers [83].

The MTF is also significantly affected by detector properties in digital imaging systems. For a CCD or CMOS sensor with a square pixel of side p (in units of λF, where λ is the wavelength and F is the f-number), the overall system MTF becomes the product of the telescope's MTF and the detector's MTF, the latter given by a sinc function: sinc(pνπ) = sin(pνπ)/(pνπ), where ν is the normalized spatial frequency [83]. This relationship means that larger pixel sizes degrade high-frequency contrast more severely, with a pixel size of p=2 causing contrast to drop to zero at a normalized spatial frequency of ν=0.5.

Wavefront Error and the Strehl Ratio

Wavefront error quantifies the deviation of an actual wavefront from its ideal shape after passing through an optical system. Measured in root-mean-square (RMS) waves or nanometers, it provides a comprehensive description of optical quality across the entire pupil. The Strehl ratio, a derivative metric, is defined as the ratio of the peak intensity in the actual point spread function to that of a perfect, diffraction-limited system [83]. A higher Strehl ratio (closer to 1) indicates better optical quality, with a commonly accepted diffraction-limited standard being a Strehl ratio of 0.80, corresponding to approximately 1/13.4 wave RMS wavefront error [83].

For complex optical systems with multiple sources of aberration, the combined wavefront error (ωc) from n individual, relatively small, and unrelated wavefront errors (ωi) is given by the root sum of squares: ωc = (Σωi²)¹ᐟ² [83]. Similarly, the combined Strehl ratio (Sc) for such aberrations can be closely approximated as the product of the individual Strehl ratios for each aberration type: Sc = S₁ × S₂ × ... × Sₙ [83]. This multiplicative relationship highlights how different aberration types compound to degrade overall system performance, underscoring the need for careful control at both component and system levels.

Table 1: Key Optical Performance Metrics and Their Characteristics

Metric	Definition	Ideal Value	Primary Significance	Measurement Techniques
MTF	Ratio of image contrast to object contrast as a function of spatial frequency	1 across all frequencies	Resolution and contrast performance	Slanted-edge method, knife-edge scan, interferometry
Strehl Ratio	Peak intensity ratio of actual PSF to diffraction-limited PSF	1	Overall optical quality; combines multiple aberrations	Interferometry, wavefront sensing, PSF measurement
Wavefront Error	RMS deviation of actual wavefront from ideal reference wavefront	0	Comprehensive description of aberrations	Shack-Hartmann sensor, interferometry, pyramid wavefront sensor
Ensquared Energy	Fraction of total point image energy contained within a specified square area	1 for square encompassing full PSF	Signal concentration for pixelated detectors	PSF measurement with calibrated aperture

Component-Level Validation: MTF and Resolution Testing

MTF Measurement Methodologies

Component-level MTF validation begins with establishing a controlled optical test bench capable of projecting precisely defined patterns onto the component under test. For lens systems and optical assemblies, the slanted-edge method is widely employed for its balance of accuracy and implementation simplicity. This technique involves imaging a precisely fabricated edge target (typically a knife-edge) with a slight angular tilt relative to the detector pixel array. The resulting oversampled edge spread function (ESF) is differentiated to obtain the line spread function (LSF), whose Fourier transform yields the MTF [83]. For systems requiring higher accuracy, interferometric MTF measurement provides a more fundamental approach by deriving the MTF directly from the wavefront data acquired using a phase-shifting interferometer.

An alternative approach suitable for microscopic objectives and endoscopic systems involves using calibrated resolution targets containing progressively finer bar patterns. The USAF 1951 target remains a common standard, where the limiting resolution is determined by the smallest group element where the line pairs remain distinguishable. However, this method provides only a binary assessment (resolvable or not) at specific frequencies rather than the continuous MTF curve, making it less comprehensive for quantitative validation. For systems operating in non-visible wavelengths, such as infrared or ultraviolet, specialized targets and detectors with appropriate spectral responses must be utilized.

Practical Implementation and Analysis

In practice, MTF measurements must be performed at multiple field points (typically on-axis, mid-field, and full-field) to fully characterize component performance. The test setup must be carefully aligned to eliminate spurious errors, with the component mounted in its intended orientation and under appropriate environmental conditions. For biomedical optics, it is often necessary to perform these measurements with the component immersed in or interfaced with appropriate media (e.g., water, matching fluid) that simulates the actual operational environment, as the refractive index mismatch can significantly alter optical performance.

Data analysis must account for the inherent MTF of the test equipment itself, which requires baseline characterization. The resulting MTF curves should be compared against design specifications and theoretical limits, with particular attention to the spatial frequency range most relevant to the intended biomedical application. For instance, fluorescence microscopy might prioritize mid-range spatial frequencies where cellular structures are typically resolved, while ophthalmoscopic systems require excellent performance at lower frequencies for contrast-rich retinal imaging. Documentation should include the complete MTF curves, not just specific data points, to provide a comprehensive performance record for validation purposes.

System-Level Validation: Wavefront Error and Aberration Analysis

Wavefront Measurement Techniques

System-level validation progresses from component-level metrics to comprehensive wavefront error analysis, which captures the overall performance of the fully integrated optical system. The Shack-Hartmann wavefront sensor is the most prevalent tool for this purpose, employing a microlens array to divide the wavefront into multiple subapertures. The local wavefront slope at each subaperture is determined by measuring the displacement of the focal spots from their reference positions, with the complete wavefront reconstructed through integration algorithms [84]. This method offers excellent dynamic range and works well with partially coherent sources common in biomedical applications.

Laser interferometry provides an alternative, higher-precision approach for systems with sufficient coherence. Phase-shifting interferometers compare the test wavefront against a reference wavefront, generating interference fringes whose phase distribution directly encodes the wavefront error. While potentially more accurate, interferometric methods are sensitive to vibration and require greater coherence, making them less suitable for some broadband biomedical light sources. Emerging techniques like the transport of intensity equation (TIE) method, which retrieves phase from through-focus intensity measurements, offer promise for systems where physical access for wavefront sensors is limited [84].

Aberration Compounding and System Tolerance Analysis

A critical aspect of system-level validation involves understanding how aberrations from individual components combine to affect overall performance. As established in the theoretical foundations, wavefront errors from multiple sources combine statistically as the root sum of squares for relatively small, uncorrelated aberrations: ωc = (ω₁² + ω₂² + ... + ωₙ²)¹ᐟ² [83]. This relationship underscores the importance of controlling even minor aberrations in individual components, as their combined effect can significantly degrade system performance. For example, in a complex system like a multi-photon microscope, aberrations from the excitation objective, scan lenses, tube optics, and detection pathway all contribute to the final wavefront error.

Tolerance analysis during the design phase establishes acceptable error budgets for each component, but system-level validation must verify that these tolerances have been met in the as-built system. This involves not only measuring the total wavefront error but also decomposing it into Zernike polynomials to identify dominant aberration types (spherical, coma, astigmatism, etc.) [85]. Such decomposition is particularly valuable for systems incorporating adaptive optics, as it informs the correction strategy. The resulting data should be compared against the established diffraction-limited standard of 1/13.4 wave RMS (0.80 Strehl ratio) or application-specific requirements that may be more or less stringent [83].

Table 2: System-Level Wavefront Error Tolerances for Diffraction-Limited Performance

Aberration Type	P-V Wavefront Error Tolerance	RMS Wavefront Error Tolerance	Primary Impact on Image Quality
Spherical	0.25 λ	0.080 λ	Symmetric blurring; reduced contrast
Coma	0.42 λ	0.080 λ	Asymmetric pointing errors; cometary tails on point sources
Astigmatism	0.37 λ	0.080 λ	Direction-dependent focus; axial asymmetry
Defocus	0.36 λ	0.080 λ	Overall blurring; reduced Strehl ratio

Advanced Protocols for Biomedical Optical Systems

Tissue-Simulating Phantoms for Validation

The validation of biomedical optical systems requires specialized protocols that account for the unique properties of biological tissues. Tissue-simulating phantoms have demonstrated their utility across the entire device life cycle, serving roles from initial proof-of-principle and design optimization to clinical trial standardization and multi-center performance monitoring [82]. These phantoms are engineered to replicate the optical properties (absorption coefficient μa, reduced scattering coefficient μs') of specific tissues across relevant wavelength ranges. Modern phantom technologies have evolved from simple homogeneous designs to sophisticated platforms incorporating biologically relevant features such as dynamic functionality, specialized optical properties like birefringence, and anthropomorphic geometry [82].

Various phantom matrix materials offer different advantages for specific applications. Silicone and epoxy resins provide excellent stability and longevity, making them ideal for reference phantoms and standardized testing [82]. Hydrogel phantoms better simulate the aqueous environment of biological tissues and can incorporate hemoglobin derivatives for more accurate representation of blood spectral properties [82]. Emerging fabrication techniques, including 3D printing with tissue-simulating materials, enable creation of anatomically realistic phantoms with complex internal structures that challenge imaging systems in biologically relevant ways [82]. The validation workflow must select appropriate phantom technology based on the specific biomedical application and validation phase.

Multi-Laboratory Performance Assessment

Establishing robust validation protocols often requires multi-laboratory assessment to ensure consistency and reproducibility across instruments and sites. Such initiatives are essential for developing reference tissue phantoms and testing protocols that are universally effective [82]. One prominent example involved 28 instruments across 12 institutions performing standardized tests based on three consolidated protocols (BIP, MEDPHOT, nEUROPt) using three kits of tissue phantoms [82]. The assessment utilized 20 synthetic indicators to comprehensively evaluate system performance, creating a benchmark for comparing different technologies and implementations.

These collaborative efforts have led to internationally recognized standards for specific biomedical optics technologies. For instance, standards now exist for pulse oximeters, cerebral oximetry, and functional near-infrared spectroscopy (fNIRS), while standardization activities are progressing for fluorescence imaging and photoacoustic imaging [82]. The implementation of these standardized phantom-based test methods provides an objective indicator of a technology's maturity and facilitates its clinical translation. For researchers developing new biomedical optical systems, adherence to these emerging standards during the validation phase significantly strengthens the credibility of their performance claims.

Implementation Workflows and Visualization

Integrated Validation Workflow

A comprehensive validation strategy for biomedical optical systems requires the systematic integration of component-level and system-level testing. The following workflow diagram illustrates the sequential yet iterative nature of this process, emphasizing the critical decision points where performance data informs progression to subsequent validation stages:

Diagram 1: Optical System Validation Workflow

This workflow begins with clearly defined system requirements derived from the intended biomedical application. Component-level testing verifies that individual optical elements meet their specified MTF and wavefront error budgets before proceeding to system integration. The critical tissue phantom validation phase assesses performance under conditions simulating real-world biological environments. Only after successful completion of all stages is the validation process documented and considered complete.

Wavefront Error Correction Process

For systems incorporating adaptive optics or requiring manufacturing compensation, the measurement and correction of wavefront errors follows an iterative process. This is particularly relevant in biomedical optics applications such as retinal imaging or deep-tissue microscopy where sample-induced aberrations must be actively compensated. The following diagram illustrates this cyclic correction process:

Diagram 2: Wavefront Error Correction Process

This iterative correction process begins with initial wavefront measurement using a Shack-Hartmann sensor or interferometer. The measured wavefront is decomposed into Zernike polynomials to identify dominant aberration types [85]. A correction signal is calculated and applied through a deformable mirror or spatial light modulator. The corrected wavefront is then re-measured to quantify residual errors, with the process repeating until wavefront quality meets the required tolerance. This approach is fundamental to adaptive optics systems used in high-resolution biomedical imaging.

Essential Research Reagent Solutions and Materials

The validation of biomedical optical systems requires specialized materials and reagents that simulate biological tissues while providing stable, reproducible properties for standardized testing. The following table catalogs key research reagent solutions essential for implementing the validation protocols discussed throughout this guide:

Table 3: Essential Research Reagents for Biomedical Optical System Validation

Reagent/Material	Composition/Type	Primary Function in Validation	Key Optical Properties
Silicone Phantoms	Polydimethylsiloxane with TiO₂ scatterers, ink absorbers	Stable reference for diffuse optical spectroscopy; standardized performance testing	Adjustable μa and μs'; excellent long-term stability [82]
Hydrogel Phantoms	Gelatin or agarose with hemoglobin derivatives	Simulation of vascularized tissues; oxygen saturation studies	Accurate blood spectrum representation; tunable water content [82]
Epoxy Resin Phantoms	Optical epoxy with scattering/absorbing particles	Long-term calibration standards; multi-laboratory comparisons	High stability; precise optical property control [82]
3D-Printed Anthropomorphic Phantoms	Photopolymer resins with optical properties	Anatomically realistic testing; system performance evaluation	Complex geometrical structures; spatially varying optical properties [82]
Dynamic Phantom Systems	Fluid channels with pumping mechanism	Simulation of physiological processes; flow imaging validation	Time-varying optical properties; programmable dynamics [82]
Resolution Test Targets	Chrome-on-glass patterns (USAF 1951, etc.)	MTF and resolution verification; system calibration	Precisely defined spatial frequencies; high contrast [83]

These research reagents enable the practical implementation of validation protocols across different stages of system development. Silicone and epoxy resin phantoms provide the stability required for reference standards and longitudinal performance monitoring, while hydrogel phantoms offer more biologically relevant environments for validating systems that measure hemodynamic parameters. The increasing sophistication of 3D-printed and dynamic phantoms addresses the growing need for validation tools that challenge imaging systems with the structural and functional complexity of living tissues.

The validation and testing protocols spanning from component-level MTF to system-level wavefront error analysis form an indispensable framework for advancing biomedical optics research. As this guide has detailed, these protocols encompass both fundamental principles—such as the statistical compounding of aberrations and the cascading impact of contrast degradation through optical and detector subsystems—and practical implementation through standardized phantom-based testing and multi-laboratory validation initiatives. The rigorous application of these protocols provides the evidence base necessary to transition promising optical technologies from laboratory demonstrations to clinically relevant tools for biological discovery and medical diagnosis.

Looking forward, the field of biomedical optics validation continues to evolve in response to emerging technologies. Computational optical sensing and imaging approaches, which tightly combine optics, sensing, and processing to acquire task-relevant information, present new validation challenges that extend beyond traditional image quality metrics [86]. Similarly, the integration of machine learning and artificial intelligence into optical systems creates new dimensions for performance assessment that must be addressed through adapted protocols. Throughout these technological transformations, the core principles established in this guide—objective quantification, standardized testing, and system-level verification—will remain essential to maintaining scientific rigor and accelerating the translation of biomedical optics innovations to impactful applications in research and clinical care.

Leveraging Expert Optics Suppliers for Robust Manufacturability and Assembly

Within the broader principles of biomedical optics research, a critical yet often underestimated phase is the transition from a functional laboratory prototype to a robust, manufacturable product. Research in this field relies on precise optical property quantification, advanced imaging techniques like Optical Coherence Elastography (OCE), and sophisticated computational sensing [87] [86]. However, the integrity of this data and the success of eventual clinical devices hinge on the mechanical and optical stability of the systems used. Challenges such as managing micron-level tolerances, compensating for thermal expansion, and correctly mounting delicate optical components are paramount [88] [89]. Engaging with expert optics suppliers who possess specialized knowledge in opto-mechanical design, precision manufacturing, and metrology is not merely a procurement strategy but a fundamental component of ensuring that research findings are translated into reliable, effective biomedical solutions. This guide details the core challenges and methodologies for leveraging this specialized expertise to overcome critical manufacturability and assembly hurdles.

Core Manufacturability and Assembly Challenges

The design of biomedical optical systems introduces distinct mechanical engineering challenges that, if unaddressed, can compromise performance and viability.

Managing Tolerances

In optical systems, minute deviations from design specifications can lead to significant performance degradation, such as blurred images or reduced signal-to-noise ratio. The types of deviations include spacing (distance between elements), tilt (angular misalignment of the optical axis), and decenter (lateral misalignment) [88]. The Hubble Space Telescope's initial blurry images, caused by a mirror ground to the wrong shape, famously exemplify the critical nature of precision, though in a non-biomedical context [88].

Solution Framework:

• Tolerance Analysis: A systematic approach is required, drawing a tolerance loop from the optical axis of one lens, through the mounting interfaces and housing components, to the next lens. Each interface and component contributes a tolerance that can be analyzed using worst-case or statistical methods [88].
• Stack Reduction: Removing components from the tolerance stack and leveraging manufacturing process strengths—such as holding tighter tolerances between features machined in the same setup—can significantly reduce cumulative error [88].
• Adjustment and Inspection: When tolerances approach manufacturing limits, designs may incorporate fine-pitch threads or ultra-fine adjustment screws for calibration. Crucially, rigorous inspection of parts is necessary to ensure they meet specifications [88].

Managing Thermals

Biomedical devices must often function across a range of ambient temperatures, which cause materials to expand and contract. This can alter critical optical distances (e.g., lens spacing, focal lengths) and, more severely, induce high stresses that fracture lenses, shear adhesive bonds, or cause stress-induced birefringence that blurs images [88].

Solution Framework:

• Material Selection: A primary strategy is to match the coefficients of thermal expansion (CTE) of the optical and mechanical materials. For instance, Calcium Fluoride optics have a CTE similar to aluminum, while Pyrex matches closely with brass. For extreme stability, alloys like Invar, with a near-zero CTE, can be used [88].
• Design for Clearance: Lens mounts must be designed with accurate constraints and sufficient clearance to accommodate differential expansion and contraction between the lens and its housing without generating damaging stresses [88].

Mounting Lenses

Lenses are brittle, rigid, and have delicate coated surfaces, making them incompatible with common fastening techniques like screws or press fits [88]. The mounting method must provide precise, stable positioning without damaging the optic.

Solution Framework: Expert suppliers utilize specialized kinematic and semi-kinematic mounting techniques that securely locate the lens while minimizing stress. These designs often use tangential contacts or compliant elastomeric rings to hold the lens, avoiding point loads that could cause fracture [88].

Table 1: Core Challenges and Supplier-Led Solutions in Optical Manufacturability

Challenge	Impact on System Performance	Key Solutions from Expert Suppliers
Tolerance Management [88]	Image blur, signal loss, failure to resolve fine features.	Statistical tolerance analysis, design for manufacturability (DFM), precision machining, and adjustment mechanisms.
Thermal Management [88]	Defocusing, changes in optical properties, lens fracture, adhesive failure.	CTE-matched material selection, thermal expansion analysis, and stress-relieving mount designs.
Lens Mounting [88]	Component damage, misalignment, introduction of stress birefringence.	Kinematic and semi-kinematic mounts, compliant adhesives, and proprietary retention techniques.
Optical Aberration Correction [89]	Distorted or blurred images, reduced measurement accuracy.	Advanced optical design software (e.g., Zemax), precision grinding/polishing, and anti-reflective coating.

Experimental Protocols for Validation

Validating the manufacturability and robustness of an optical system requires rigorous testing. The following methodologies are essential.

Protocol for Tolerance Stack Analysis

This protocol verifies that the cumulative effect of all part tolerances does not push the system out of its performance budget.

• Define the Optical Performance Budget: Establish the maximum allowable wavefront error or modulation transfer function (MTF) degradation.
• Identify the Tolerance Loop: Select a critical path in the assembly, such as the distance and alignment between two key lenses [88].
• Model the Loop: Use optical design software (e.g., Zemax) to model the system. Assign realistic tolerances to each parameter in the loop (e.g., surface curvature, thickness, position) based on the supplier's capabilities [89].
• Perform Monte Carlo Analysis: Run a statistical simulation (e.g., 1000 iterations) that randomly varies all parameters within their tolerance ranges to predict the distribution of system performance [89].
• Iterate on Design: If the analysis shows an unacceptable probability of performance loss, tighten critical tolerances or redesign the mount to reduce the stack-up.

Protocol for Thermal Stability Testing

This protocol assesses system performance across its specified operating temperature range.

• Establish Baseline Performance: Measure key performance metrics (e.g., focus sharpness, resolution target imaging) at a standard room temperature (e.g., 20°C).
• Place System in Environmental Chamber: Secure the optical system in a thermal chamber capable of controlling temperature.
• Execute Thermal Cycling: Subject the system to a defined temperature profile, for example, from -10°C to +50°C, with suitable dwell times at extremes to ensure thermal equilibrium [88].
• Measure Performance at Intervals: At set temperature points during both ramp-up and cool-down, repeat the performance measurements established in Step 1.
• Post-Test Inspection: Upon completion of the cycle, inspect the system for physical damage, such as cracked lenses or failed adhesive bonds.

Thermal Testing Workflow

The Scientist's Toolkit: Research Reagent Solutions for Biomedical Optics

The following materials and tools are essential for developing and validating biomedical optical systems, where standardized phantoms and characterization tools serve as the "reagents" for ensuring quantitative accuracy.

Table 2: Essential Research Reagents and Materials for Biomedical Optics

Item	Function & Explanation
Tissue-Equivalent Optical Phantoms [90]	Serve as standardized reference targets with known optical properties (e.g., absorption, scattering) to calibrate imaging systems (e.g., OCT, diffuse optics) and validate performance before clinical use.
Time-of-Flight (ToF) Characterization Systems [90]	Provide a gold-standard, independent method for quantifying the optical properties of phantoms and tissues, enabling cross-validation of other broadband measurement techniques.
Optical Design & Analysis Software (Zemax) [89]	Used to design, analyze, and optimize optical systems via ray tracing; performs critical tolerance analysis to assess the impact of manufacturing variations on performance.
Optical Coherence Elastography (OCE) [87]	A functional extension of OCT that maps tissue biomechanical properties (stiffness) with micrometer-scale resolution, providing a non-invasive method for assessing tissue health.

A Framework for Supplier Collaboration and Selection

Success in transitioning a biomedical optical system from research to production depends on a strategic approach to engaging with expert suppliers.

• Define Critical-to-Function Parameters: Clearly identify the non-negotiable optical and mechanical performance metrics for your system. This focuses discussions with suppliers on what truly matters.
• Seek Partners with Specialized Metrology: Prioritize suppliers who possess and can demonstrate expertise in the specific characterization methods your field relies on, such as time-of-flight systems for quantitative biophotonics or specialized interferometers for wavefront measurement [90].
• Evaluate DFM/A Capability: Assess the supplier's ability to perform Design for Manufacturability and Assembly (DFM/A) reviews. They should proactively suggest tolerance relaxations, material substitutions, and design modifications that enhance robustness without compromising function [88] [89].
• Leverage Cross-Border Innovation Ecosystems: Tap into regional clusters of expertise, such as the optics and photonics corridor uniting Vermont and Québec, which hosts a concentration of leaders in precision optics and photonics, from research institutes to commercial manufacturers [90].

Supplier Selection Strategy

The path from a pioneering concept in biomedical optics to a reliable, mass-producible instrument is fraught with intricate opto-mechanical challenges. A deep understanding of core research principles must be coupled with an equally deep appreciation for the disciplines of precision engineering and manufacturing. Proactively collaborating with expert optics suppliers who bring validated metrology, mastery of materials, and specialized manufacturing knowledge is not a mere procedural step; it is a strategic imperative. This partnership is the surest way to navigate the complexities of tolerance stacks, thermal dynamics, and delicate component integration, thereby ensuring that innovative biomedical optics research achieves its ultimate goal: creating standardized, reproducible, and impactful tools for advancing human health.

Benchmarking Biomedical Optics: Validation, Contrast, and Multi-Modal Integration

Within the broader thesis on the basic principles of biomedical optics research, understanding the landscape of established medical imaging technologies is foundational. While biomedical optics leverages light-based technologies for diagnosis and research, modalities like Magnetic Resonance Imaging (MRI), Computed Tomography (CT), and Positron Emission Tomography (PET) represent critical, complementary pillars of modern biomedical imaging. This guide provides a detailed technical comparison of these three core modalities, framing their respective strengths and limitations to inform researchers and drug development professionals. The choice between these imaging technologies is pivotal in both clinical and research settings, as it directly impacts data quality, the specific biological questions that can be addressed, and ultimately, the efficacy of therapeutic development [91]. This analysis will detail the fundamental principles, operational parameters, and specific applications of each, providing a structured reference for selecting the optimal tool for a given research or diagnostic objective.

Fundamental Principles and Technical Specifications

The core technologies of MRI, CT, and PET are based on distinct physical principles, which directly dictate the type of information they yield and their appropriate applications.

• Computed Tomography (CT): CT scanners utilize X-rays, a form of ionizing radiation, to generate detailed cross-sectional images of the body. The patient passes through a rotating X-ray tube and detector assembly, and a computer reconstructs the attenuation data into anatomic images. The key strength of CT lies in its high spatial resolution for dense structures like bone and its rapid acquisition speed, making it indispensable in emergency settings [92] [91]. However, its reliance on ionizing radiation and its limited soft-tissue contrast compared to MRI are significant limitations [93].

• Magnetic Resonance Imaging (MRI): MRI employs powerful magnetic fields and radiofrequency pulses to interact with hydrogen nuclei (primarily in water and fat) within the body. The signals emitted during relaxation are used to construct images. The major advantage of MRI is its unparalleled soft-tissue contrast without using ionizing radiation, making it the gold standard for imaging the brain, spinal cord, and musculoskeletal system [92] [91]. Its limitations include longer scan times, sensitivity to patient motion, and safety concerns for individuals with certain metallic implants [93] [91].

• Positron Emission Tomography (PET): PET is a functional imaging modality that visualizes metabolic processes. It requires the administration of a radioactive tracer. The most common tracer is 18F-fluorodeoxyglucose (18F-FDG), a glucose analog that accumulates in cells with high metabolic activity, such as cancer cells. The decay of the tracer produces gamma rays that are detected to create a metabolic map of the body [92] [91]. PET's primary strength is its ability to detect disease at a cellular level, often before structural changes are visible. Its main weakness is poor anatomical detail, which is why it is almost always combined with CT or MRI in hybrid systems (PET/CT or PET/MRI) to fuse metabolic and anatomic information [93] [91].

Table 1: Core Physical Principles and Clinical Strengths

Modality	Fundamental Principle	Primary Clinical & Research Strengths
Computed Tomography (CT)	X-ray attenuation and computer reconstruction	High-speed acquisition; excellent bone detail; ideal for trauma, stroke, and lung imaging [92] [91]
Magnetic Resonance Imaging (MRI)	Nuclear magnetic resonance of hydrogen nuclei	Superior soft-tissue contrast; no ionizing radiation; excellent for neurology and musculoskeletal imaging [93] [92]
Positron Emission Tomography (PET)	Detection of gamma rays from positron-emitting radiotracers	Reveals metabolic/functional activity; sensitive for cancer detection, dementia, and epilepsy [92] [91]

Quantitative Performance Data and Comparison

To objectively compare the diagnostic performance of these modalities, particularly in oncology, meta-analyses provide robust evidence. The following table synthesizes recent findings on their accuracy in detecting distant metastases and staging specific cancers.

Table 2: Comparative Diagnostic Performance in Oncology

Modality & Application	Reported Sensitivity	Reported Specificity	Notes & Context
PET/MRI (Distant Metastases, various cancers) [94]	0.87 (Pooled)	0.97 (Pooled)	Demonstrates high overall accuracy for metastatic staging.
PET/CT (Distant Metastases, various cancers) [94]	0.81 (Pooled)	0.97 (Pooled)	High specificity, but slightly lower sensitivity than PET/MRI.
PET/MRI (Breast Cancer Metastases) [94]	0.95	0.96	Outperforms PET/CT in this specific cancer type.
PET/CT (Lung Cancer Metastases) [94]	0.87	0.95	Holds an advantage over PET/MRI for lung metastases.
MRI (Multiple Myeloma Staging) [95]	0.914	N/A*	Superior sensitivity to PET/CT for initial staging.
PET/CT (Multiple Myeloma Staging) [95]	0.807	N/A*	Lower sensitivity than MRI; 14% of patients had negative PET/CT but positive MRI [95].

Note: Specificity was not consistently reported in the multiple myeloma meta-analysis due to a need for standardized definitions across studies [95].

Beyond pure diagnostic accuracy, operational factors are critical for research workflow and clinical planning. A prospective study in gynecologic cancer found that an integrated PET/MRI exam significantly reduced the average total imaging time to 180.3 minutes, a 38.1% reduction compared to the 291.2 minutes required for sequential PET/CT and MRI [96]. This demonstrates a substantial workflow efficiency for combined modalities.

Experimental and Operational Considerations

Detailed Methodologies for Comparative Studies

The quantitative data presented in Section 3 are derived from rigorous experimental protocols. A typical methodology for a comparative study of PET/CT versus PET/MRI in oncology involves the following steps [96] [94]:

• Patient Cohort: Enrollment of patients with a known malignancy (e.g., gynecologic, breast, or lung cancer) confirmed by histopathology.
• Imaging Protocol: Patients undergo both PET/CT and PET/MRI scans in a single session or consecutively within a short timeframe after a single injection of the radiotracer (e.g., 18F-FDG).
• Image Acquisition:
  • PET/CT: A low-dose CT scan is first acquired for attenuation correction and anatomical localization, followed by the PET acquisition.
  • PET/MRI: Simultaneous PET and MRI data are acquired. The MRI protocol typically includes T1-weighted, T2-weighted, and Diffusion-Weighted Imaging (DWI) sequences. A key technical challenge is generating an accurate attenuation correction map from MRI data, as MRI does not directly measure tissue density like CT [93].
• Image Analysis: Images are independently evaluated by experienced radiologists/nuclear medicine physicians blinded to the other modality's results. They assess parameters like primary tumor delineation, lymph node involvement, and distant metastases.
• Reference Standard: Findings are confirmed by a reference standard, which may include histopathological analysis of biopsied or resected tissue and/or imaging follow-up (e.g., interval growth on subsequent scans) [94].
• Statistical Analysis: Diagnostic performance metrics (sensitivity, specificity) are calculated for each modality. Statistical tests like McNemar's test are used to compare the accuracy, and Cohen's Kappa may be used to evaluate inter-rater agreement [96].

The Scientist's Toolkit: Key Reagents and Materials

The following table details essential materials used in the featured PET-based imaging experiments.

Table 3: Research Reagent Solutions for PET-based Imaging

Item	Function in Experiment
18F-FDG Radiotracer	The primary imaging probe; a glucose analog that accumulates in metabolically active cells, allowing for the detection of tumors and metastases [94] [91].
MRI Contrast Agents (e.g., Gadolinium-based)	Used to enhance vascular structures and tissues, improving the detection and characterization of lesions in both standalone MRI and the MRI component of PET/MRI [93].
CT Iodinated Contrast Agent	Injected to enhance blood vessels and organ parenchyma during the CT portion of a PET/CT scan, improving anatomic delineation.
Attenuation Correction Phantoms	Specialized devices used to calibrate the scanners and ensure the quantitative accuracy of PET data by correcting for photon attenuation, a particular challenge in PET/MRI [93].

Integrated Workflows and Decision Pathways

The choice between MRI, CT, and PET is driven by the specific biological or clinical question. The following diagram outlines a high-level decision workflow for selecting an imaging modality in a research or diagnostic context.

Hybrid systems like PET/CT and PET/MRI integrate functional and anatomical information, each with distinct advantages. PET/CT is widely available, has established protocols, and is excellent for imaging pulmonary nodules [93]. PET/MRI, while less available, offers superior soft-tissue contrast, the added value of functional MRI sequences like DWI, and reduced ionizing radiation, making it particularly advantageous for cancers in the liver, pelvis, and brain, as well as for pediatric populations [93] [94]. A key operational advantage of PET/MRI is workflow efficiency; it provides a one-stop-shop for combined metabolic and high-quality anatomic imaging, significantly reducing the total patient time in the department compared to sequential PET/CT and MRI [96].

The comparative analysis of MRI, CT, and PET reveals a landscape of complementary, rather than competing, technologies. CT provides unparalleled speed and bony detail, MRI excels in soft-tissue characterization without radiation, and PET offers a unique window into cellular metabolism. The emerging paradigm of hybrid imaging, particularly PET/MRI, combines the strengths of functional and multiparametric anatomic imaging, showing superior diagnostic performance in specific cancers and offering significant workflow benefits. For researchers and drug development professionals, the selection of an imaging modality must be a deliberate decision based on the specific biological question, the required balance between structural and functional data, and practical considerations of workflow and quantitative accuracy. As imaging technologies continue to evolve, their integration with emerging fields like biomedical optics will further empower the precise detection, monitoring, and understanding of disease.

The validation of functional hemodynamic data against established gold standards is a critical process in biomedical optics research, ensuring that advanced imaging techniques accurately represent underlying physiological phenomena. This technical guide examines the core principles and methodologies for correlating two-dimensional optical spectroscopic imaging with reference techniques, focusing on the quantification of cerebral hemodynamics. We explore the experimental frameworks for validating hemodynamic parameters, discuss the inherent limitations of optical techniques, and present standardized protocols for establishing functional correlations. Within the broader thesis of biomedical optics, this review emphasizes the critical importance of rigorous validation to bridge innovative optical methodologies with physiologically relevant measurements, thereby enabling reliable interpretation of hemodynamic responses in both research and clinical applications.

Optical intrinsic signal (OIS) imaging and related spectroscopic techniques have become indispensable tools in functional brain imaging, providing high-resolution spatial and temporal data on cerebral hemodynamics. These perfusion-based modalities measure changes in cortical light reflectance that arise from various biological processes, including hemoglobin absorption and light scattering due to cellular activity and vascular changes [97] [98]. Unlike direct neuronal recording techniques, hemodynamic-based imaging requires careful interpretation to relate measured signals to underlying neural activity, creating a fundamental need for validation against established physiological measurement standards.

The transition from single-wavelength OIS imaging to two-dimensional optical spectroscopy (2DOS) represents a significant methodological advancement. While traditional OIS imaging adds a layer of convolution between measured signals and their physiological sources, 2DOS acquires images at multiple wavelengths and applies spectroscopic analysis at each pixel, generating functional images of hemoglobin oxygenation and blood volume changes with greater biological relevance [98]. This approach combines the spatial advantages of imaging with the physiological specificity of spectroscopy, but introduces several important assumptions that require rigorous validation.

Core Validation Challenges in correlating optical hemodynamics with gold standards primarily stem from technical and physiological factors. The reduced spectral resolution of 2DOS compared to full-spectrum fiber spectroscopy, combined with temporally staggered data acquisition across wavelengths, creates potential discrepancies that must be quantified [97]. Furthermore, the complex light-tissue interactions in biological systems, where photons follow zigzag paths through highly scattering media, complicate direct interpretation of optical signals without appropriate mathematical modeling and experimental correlation [99].

Gold Standard Techniques in Hemodynamic Assessment

Traditional Fiber Spectroscopy

Fiber spectroscopy stands as the established reference methodology for quantifying functional hemodynamic changes in tissue. Over the past decade, this technique has demonstrated consistent fidelity in representing hemodynamic responses across diverse experimental models [98]. The fundamental strength of fiber spectroscopy lies in its comprehensive spectral resolution—it decomposes reflected light over a full spectral axis, enabling detailed curve fitting to physiological models of hemoglobin absorption and oxygenation.

The technical implementation of fiber spectroscopy involves placing a fiber optic bundle in direct contact with the tissue region of interest. This setup captures complete reflectance spectra across a broad wavelength range simultaneously, providing a robust dataset for quantifying concentrations of oxyhemoglobin (HbO2), deoxyhemoglobin (Hbr), and total hemoglobin (Hbt) without temporal staggering between wavelength measurements [97]. This simultaneity of data acquisition eliminates potential artifacts caused by physiological timing variations, establishing fiber spectroscopy as a temporally precise reference method.

Fractional Flow Reserve in Vascular Assessment

In coronary hemodynamics, fractional flow reserve (FFR) has emerged as the clinical gold standard for estimating functional stenosis significance [100]. This invasive wire-based technique directly measures pressure gradients across coronary lesions during maximal blood flow (hyperemia), providing a physiologically validated index for ischemia-producing blockages. While applied in different vascular beds than cerebral optical imaging, the principles of FFR validation inform best practices across hemodynamic assessment methodologies, particularly in establishing clinical correlation for technically derived measurements.

Experimental Validation Framework for 2DOS

Concurrent Validation Methodology

A robust experimental framework for validating two-dimensional optical spectroscopy involves simultaneous acquisition of 2DOS and fiber spectroscopy data during controlled physiological interventions. The core protocol entails measuring hemodynamic responses to standardized stimuli—such as hindpaw electrical stimulation in rodent models—while concurrently recording multi-wavelength images and fiber spectroscopy data from the same somatosensory cortex region [97] [98]. This parallel acquisition enables direct point-by-point comparison between the techniques under identical physiological conditions.

Animal Preparation Protocol: Validation experiments typically utilize appropriate animal models (e.g., Sprague-Dawley rats) following institutional animal care guidelines. Key preparation steps include:

• Surgical exposure and thinning of the skull over the region of interest
• Application of silicone oil to increase bone translucency for optical access
• Administration of anesthesia maintenance (e.g., intravenous alpha-chloralose) and neuromuscular blockade to minimize movement artifacts
• Stabilization of physiological parameters (blood pressure, temperature, blood gases) throughout the experimental procedure

Data Acquisition Parameters: Concurrent 2DOS and fiber spectroscopy data should be collected using these standardized settings:

• 2DOS Imaging: Sequential acquisition at four discrete wavelengths (e.g., 560, 570, 580, and 590 nm) using a scientific-grade CCD camera
• Fiber Spectroscopy: Continuous full-spectrum measurement (500-630 nm) from a fiber bundle placed adjacent to the imaging field
• Stimulation Protocol: Controlled electrical stimulation (e.g., 3 mA, 0.3 ms pulse width, 3 Hz) delivered for 4-second duration with adequate inter-trial intervals
• Trial Structure: Minimum of 20 trials per condition with interleaved wavelength acquisition to minimize systematic timing artifacts

Analytical Correlation Methods

The correlation between 2DOS and gold standard measurements requires specialized analytical approaches to quantify agreement and identify potential systematic biases.

Spectroscopic Analysis: Both 2DOS and fiber spectroscopy data are fit to the same modified Beer-Lambert law model incorporating wavelength-dependent absorption coefficients for HbO2 and Hbr. The model calculates concentration changes for each hemoglobin species based on measured reflectance changes at each wavelength [98].

Statistical Correlation Framework: Time-course data for each hemodynamic parameter (ΔHbO2, ΔHbr, ΔHbt) should be compared using:

• Linear regression analysis at each time point
• Calculation of Pearson's correlation coefficients (r) for response magnitudes
• Analysis of fitting residuals to identify wavelength-specific discrepancies
• Signal-to-noise ratio comparisons between techniques

Table 1: Correlation Metrics Between 2DOS and Fiber Spectroscopy

Hemodynamic Parameter	Correlation Coefficient (r)	Fitting Residuals	Signal-to-Noise Ratio Difference
ΔHbO2 (Oxyhemoglobin)	0.85-0.92	2.8-4.1%	22-31% lower in 2DOS
ΔHbr (Deoxyhemoglobin)	0.79-0.87	3.2-5.3%	18-27% lower in 2DOS
ΔHbt (Total Hemoglobin)	0.82-0.90	2.5-3.8%	25-33% lower in 2DOS

Visualization and Interpretation of Validated Data

Parameterized Color Mapping

Effective visualization of correlated hemodynamic data requires integrated display methods that concisely represent multiple parameters. A three-parameter color mapping strategy assigns HbO2, Hbr, and Hbt to individual RGB color channels, generating composite images that display the spatiotemporal evolution of hemodynamic responses [97] [98]. This approach enables simultaneous visualization of oxygenation and volume changes through parenchymal and vascular compartments in a single image sequence.

The color mapping protocol involves:

• Channel Assignment: ΔHbO2 → Red channel, ΔHbr → Green channel, ΔHbt → Blue channel
• Intensity Normalization: Each parameter is normalized to its maximum response amplitude across the time series
• Composite Generation: RGB values are calculated for each pixel and time point
• Temporal Encoding: Time-series data is displayed as a sequence or overlayed with temporal color gradients

This visualization strategy successfully encapsulates the complex multidimensional data obtained from validated 2DOS experiments, facilitating interpretation of hemodynamic propagation patterns and compartment-specific responses.

Experimental Workflow Integration

The complete validation and analysis workflow integrates multiple technical and analytical components into a standardized processing pipeline, as illustrated below:

Advanced Computational Validation Methods

Computational Fluid Dynamics in Hemodynamic Validation

Computational fluid dynamics (CFD) provides a powerful mathematical framework for validating optical hemodynamic measurements through physics-based simulation. CFD techniques apply numerical methods to solve the Navier-Stokes equations governing blood flow in reconstructed three-dimensional vascular models [100]. When applied to optical imaging data, CFD creates simulated hemodynamic parameters that can be directly compared to experimentally measured values, serving as a computational gold standard.

The CFD validation workflow involves three critical stages:

• Pre-processing: 3D reconstruction of coronary/cerebral arteries from medical images and mesh generation
• Solver Implementation: Application of fluid properties (blood density: 1050 kg/m³, viscosity: 3.5×10⁻³ Pa·s) and boundary conditions
• Post-processing: Extraction of hemodynamic parameters (pressure gradients, flow velocities) for correlation with optical measurements

CFD-based validation has demonstrated particular utility in coronary hemodynamics, where virtual FFR assessment shows 89% diagnostic accuracy at the per-patient level compared to invasive measurement [100]. This computational approach provides a valuable bridge between optical measurements and physiological significance, especially for complex hemodynamic patterns in diseased vasculature.

Boundary Conditions and Assumptions

Computational validation methods require careful implementation of boundary conditions that represent physiological states. Key considerations include:

Flow Conditions: Application of resting or hyperemic flow rates based on experimental paradigm Vascular Properties: Treatment of vessel walls as distensible structures with appropriate material properties Fluid Modeling: Selection of Newtonian (constant viscosity) or non-Newtonian (shear-dependent viscosity) blood models Microvascular Resistance: Implementation of appropriate downstream resistance values based on physiological measurements

Table 2: Boundary Conditions for CFD Validation of Optical Hemodynamics

Boundary Condition	Resting State Value	Hyperemic State Value	Physiological Basis
Aortic Pressure (Inlet)	90-100 mmHg	90-100 mmHg	Mean arterial pressure
Coronary Flow Reserve	1.0 (baseline)	2.5-4.0 × baseline	Pharmacologic stimulation
Microvascular Resistance	High	Low	Autoregulatory response
Blood Viscosity	3.5 × 10⁻³ Pa·s	3.5 × 10⁻³ Pa·s	Newtonian approximation

The Scientist's Toolkit: Research Reagent Solutions

Successful validation of optical hemodynamic data requires specialized materials and analytical tools. The following table details essential research reagents and their functions in experimental protocols:

Table 3: Essential Research Reagents for Optical Hemodynamic Validation

Reagent/Material	Function	Application Notes
Alpha-chloralose Anesthesia	Maintenance of stable physiological state during experiments	Preserves neurovascular coupling compared to other anesthetics; initial bolus 60 mg/kg, infusion 30 mg/kg/h [98]
Pancuronium Bromide	Neuromuscular blockade for motion control	Prevents movement artifacts during optical imaging; 2 mg initial dose, 1 mg/kg/h maintenance [98]
Silicone Oil	Optical clearing agent for bone	Increases translucency of thinned skull preparation; improves light transmission for deeper imaging [97]
Physiological Saline	Maintenance of tissue hydration and ionic balance	Continuous application to prevent tissue drying during prolonged experiments
Artificial Cerebrospinal Fluid	Physiological medium for cortical surface	Maintains ionic homeostasis when direct cortical exposure is required
Fluorescent Microspheres	Blood flow reference standard	Validation of perfusion measurements against absolute flow standards
Enzyme Inhibitors (L-NAME, etc.)	Pharmacologic manipulation of vascular tone	Investigates specific pathways in neurovascular coupling

Limitations and Methodological Considerations

Despite strong correlation with gold standard techniques, optical hemodynamic validation faces several important limitations that researchers must address in experimental design and interpretation.

Spectral Resolution Trade-offs: The fundamental compromise in 2DOS involves reduced spectral resolution compared to fiber spectroscopy. While fiber spectroscopy decomposes reflected light over a full spectral axis, 2DOS retains spatial dimensions by acquiring images at only a few wavelengths [97]. This reduction necessitates careful selection of optimal wavelengths that provide maximal discrimination between hemoglobin species while maintaining acceptable signal-to-noise ratios.

Temporal Displacement Artifacts: 2DOS data acquisition typically involves sequential capture at different wavelengths within or between trials, combined during analysis as if acquired simultaneously [98]. This temporal staggering can introduce artifacts during dynamic hemodynamic responses, particularly for stimuli with rapid onset. Sufficient trial averaging (typically >20 repetitions) is required to compensate for this limitation, potentially obscuring single-trial response characteristics.

Signal-to-Noise Considerations: Comparative analyses consistently demonstrate lower signal-to-noise ratios for 2DOS data compared to fiber spectroscopy [97]. This difference stems from the spatial distribution of detection in imaging approaches versus integrated light collection in fiber-based systems. The noise characteristics particularly affect deoxyhemoglobin measurements due to its lower concentration changes and more subtle optical effects.

Light Scattering Complications: Modeling light transport in tissue remains challenging due to high scattering properties. The Monte Carlo technique provides a flexible method for simulating photon propagation through complex inhomogeneous media [99], but requires accurate optical property inputs that may vary between tissue regions and physiological states.

Future Directions in Hemodynamic Validation

The field of optical hemodynamic validation continues to evolve with advancements in imaging technology, computational methods, and molecular tools. Promising directions include:

Multi-Modal Integration: Combining optical hemodynamic imaging with complementary techniques such as simultaneous fMRI or electrophysiology provides cross-validation across modalities with different physical bases and limitations.

Advanced Tissue Clearing Techniques: Methods such as CUBIC, CLARITY, and vDISCO enable whole-organ optical access while preserving fluorescent protein signals [101]. These approaches facilitate validation across spatial scales from cellular resolution to entire networks.

Machine Learning Enhancement: Artificial intelligence approaches show promise for improving spectroscopic analysis accuracy, particularly in cases with limited spectral sampling or elevated noise levels.

Microvascular Resolution Validation: Development of ultra-high resolution techniques enables correlation of optical measurements with microscopic vascular anatomy, bridging the gap between bulk hemodynamic signals and their microvascular sources.

As optical imaging technologies continue to advance, maintaining rigorous validation frameworks against physiological gold standards remains essential for ensuring that new methodologies provide accurate, biologically relevant insights into cerebral hemodynamics and neurovascular function.

Biomedical optics research relies on the ability to visualize biological processes at the molecular, cellular, and tissue levels. This capability is enabled by various contrast mechanisms that differentiate target structures from their surrounding environment. These mechanisms can be broadly categorized into intrinsic and extrinsic approaches. Intrinsic contrast leverages naturally occurring optical properties of tissues and biomolecules, such as absorption by hemoglobin or light scattering from cellular structures [102]. This approach enables non-invasive observation without introducing external agents, making it valuable for clinical diagnostics and fundamental biological studies. For instance, blood oxygen level-dependent (BOLD) contrast in functional magnetic resonance imaging (fMRI) capitalizes on intrinsic paramagnetic properties of deoxygenated hemoglobin to map brain activity [102].

In contrast, extrinsic contrast employs exogenous probes introduced into the biological system to enhance visualization of specific targets. These include small-molecule dyes, nanoparticles, and genetically encoded reporters that bind to or are expressed in specific cells and molecules [103] [104]. The development of novel extrinsic probes represents a thriving area of research, continually expanding the possibilities for observing and quantifying biological processes. Molecular imaging combines these probes with advanced imaging technologies, allowing researchers to visualize cellular processes in living subjects at the molecular level [105]. This technical guide examines the fundamental principles, applications, and methodologies of both intrinsic and extrinsic contrast mechanisms, with particular emphasis on genetic reporter systems that have revolutionized modern biomedical research.

Fundamental Principles of Intrinsic Contrast

Physical Origins and Mechanisms

Intrinsic contrast in biomedical imaging arises from the inherent interactions between light and biological tissues without exogenous labeling. These interactions include absorption, scattering, fluorescence, and reflectance, each providing information about tissue composition and structure. A prime example of intrinsic contrast is the BOLD effect in functional MRI, where deoxygenated blood acts as an endogenous paramagnetic contrast agent, suppressing the T2* signal [102]. When neural activity increases blood flow and oxygenation, the T2* signal increases, enabling mapping of brain function without external contrast agents.

The versatility of intrinsic contrast mechanisms is particularly evident in magnetic resonance imaging (MRI), where the relationship between image signal and the physical-chemical properties of matter allows generation of multiple image contrasts [106]. The signal intensity (SI) in MRI reflects contributions from both intrinsic parameters (longitudinal and transverse relaxation times T1 and T2, proton density, diffusion coefficients) and extrinsic parameters (equipment characteristics, pulse sequences, timing parameters) [106]. This relationship can be summarized by the equation:

[ S = \rho \cdot (1 - e^{-TR/T1}) \cdot e^{-TE/T2} \cdot e^{-bD} ]

Where ( \rho ) represents proton density, TR is repetition time, TE is echo time, and D is the diffusion coefficient with b-factor representing diffusion weighting [106]. This complex relationship enables MRI to generate various contrast weightings including T1-weighted, T2-weighted, proton density, and diffusion-weighted images, each highlighting different tissue properties without external contrast agents.

Applications and Limitations in Research

Intrinsic contrast mechanisms find application across numerous research domains. In neuroimaging, fMRI with BOLD contrast localizes brain regions active during specific behaviors or cognitive tasks using block designs that alternate between active and baseline conditions [102]. In somatosensation research, the high density of intrinsic mechanoreceptors in glabrous skin regions like fingertips and tongues enables detailed tactile sensitivity studies without exogenous probes [102].

However, intrinsic contrast faces several limitations. The T2* imaging used in BOLD fMRI suffers from susceptibility artifacts near air-tissue interfaces, causing signal loss in inferior temporal lobe regions [102]. Vascular uncoupling near vascular lesions can alter the typical hemodynamic response, complicating interpretation [102]. Furthermore, many intrinsic contrast mechanisms offer limited specificity for molecular targets compared to extrinsic approaches, restricting their utility for probing specific cellular pathways or molecular events.

Extrinsic Probe-Based Contrast Mechanisms

Design Principles and Classification

Extrinsic probes are engineered to bind specifically to molecular targets or accumulate in particular cellular compartments, generating contrast through various mechanisms. These probes can be classified by their physical mechanism (absorbing, fluorescent, photoswitchable), composition (small molecules, nanoparticles, proteins), or application (structural, functional, molecular). A critical distinction exists between directly detected probes and those that produce contrast through enzymatic activity.

Small-molecule dyes represent a well-established category of extrinsic probes. In protein aggregation studies, dyes like thioflavin T (ThT), pentameric formylthiophene acetic acid (pFTAA), and PicoGreen bind to amyloid structures with high specificity [103]. Upon binding to β-sheet structures, ThT experiences a dramatic increase in quantum yield by multiple orders of magnitude (from 10⁻⁴ to 0.83 with insulin fibrils), enabling sensitive detection of protein aggregates [103]. These probes can be used in single-molecule detection systems to characterize heterogeneous aggregate populations formed during the aggregation process of proteins like α-synuclein, associated with Parkinson's disease [103].

Experimental Implementation with Extrinsic Probes

The application of extrinsic probes requires careful optimization of experimental conditions. For single-molecule detection of protein aggregates using extrinsic dyes, the protocol involves several critical steps:

• Probe Preparation: Stock solutions of dyes like ThT are prepared in appropriate buffers (e.g., 25 mM Tris, 100 mM NaCl, pH 7.4) with concentrations determined spectrophotometrically using known extinction coefficients (36,000 M⁻¹·cm⁻¹ for ThT at 412 nm) [103].

• Sample Incubation and Labeling: Protein monomers are incubated under aggregating conditions, with aliquots taken at regular intervals and diluted to nanomolar concentrations (20 nM) in buffer containing the chosen extrinsic dye [103].

• Single-Molecule Detection: Diluted samples flow through microfluidic devices at controlled velocities (0.56 cm·s⁻¹) for detection via confocal microscopy with appropriate laser excitation (445 nm for ThT, 488 nm for pFTAA) and emission filtering [103].

This approach enables quantification of aggregate numbers and provides structural insights through analysis of dye emission intensity, which correlates with β-sheet content and other structural elements to which specific dyes are sensitive [103].

Table 1: Properties of Selected Extrinsic Dyes for Protein Aggregation Studies

Dye Name	Absorption Maximum (nm)	Extinction Coefficient (M⁻¹·cm⁻¹)	Binding Target	Signal Enhancement Upon Binding
Thioflavin T (ThT)	412	36,000	β-sheet structures	Quantum yield increases from 0.0001 to 0.83
diThT-PEG2	410	45,800	β-sheet structures	Similar to ThT with potentially improved binding
pFTAA	~450-500	Not specified	Amyloid structures	Large increase upon binding to aggregates
PicoGreen	~500	Not specified	DNA	Large increase when bound to double-stranded DNA

Figure 1: Generalized Workflow for Extrinsic Probe-Based Contrast Mechanisms

Genetic Reporter Systems for Contrast Generation

Fundamental Concepts and Design Strategies

Genetic reporter systems represent a powerful category of extrinsic contrast mechanisms where contrast is generated by proteins encoded by introduced genetic sequences. These systems enable visualization of specific cellular processes, including gene expression, protein localization, and cell fate. Reporter gene/reporter probe technology provides a generalizable method for noninvasive imaging of protein expression, protein function, and protein-protein interactions [105].

A sophisticated example is the Bivalent Enhanced Traffic Light Editing (BETLE) reporter system, which incorporates multiple reporter proteins in different open-reading frames to detect CRISPR/Cas genome editing outcomes [107]. The system constitutively expresses mCherry-P2A-ΔmoxGFP, followed by out-of-frame P2A-mTagBFP2 (N-2 ORF) and T2A-NanoLuc (N-1 ORF) cassettes. Out-of-frame editing through non-homologous end joining (NHEJ) leads to expression of either intracellular mTagBFP2 or secreted NanoLuc, providing both spatial localization and highly sensitive luminescence readouts [107]. Successful homology-directed repair (HDR) is detected through restoration of functional moxGFP expression [107].

Implementation Across Imaging Modalities

Genetic reporters have been adapted for diverse imaging modalities, each with unique requirements and capabilities:

Optical Imaging: The herpes simplex virus type-1 thymidine kinase (HSV1-tk) reporter gene with radioactive probes like 9-(4-18F-fluoro-3-[hydroxymethyl]butyl)guanine ([18F]FHBG) can be imaged using optical techniques that detect Cerenkov radiation emitted by radioactive decay [105]. This approach enables optical monitoring of nuclear reporter probes with high correlation to gamma counting results (r² > 0.95) [105].

Photoacoustic Imaging (PAI): Genetic reporters for PAI include enzymatic reporters (e.g., tyrosinase producing eumelanin), fluorescent proteins (e.g., EGFP, DsRed), and specialized chromoproteins [104]. These can be introduced via transient transfection (chemical methods using cationic liposomes/lipids or calcium phosphate) or stable transduction (lentiviral or retroviral vectors) [104]. The ideal PAI reporter should have high absorption in the tissue optical window, low toxicity, and minimal photobleaching [104].

RNA-Based Detection: Intronic RNAscope probes target intronic regions of pre-mRNAs to specifically identify nuclei of specific cell types, such as cardiomyocytes [108]. This approach overcomes limitations of antibody-based nuclear identification, with Tnnt2 intronic probes showing high specificity for cardiomyocyte nuclei even during mitosis with nuclear envelope breakdown [108].

Table 2: Genetic Reporters for Different Imaging Modalities

Imaging Modality	Reporter Gene	Reporter Probe/Substrate	Detection Method	Applications
Optical/Bioluminescence	Luciferase	D-luciferin, Coelenterazine	Photon detection	Monitoring gene expression, cell tracking
Optical/Fluorescence	EGFP, mCherry	None (autofluorescent)	Fluorescence imaging	Protein localization, gene expression
Nuclear Imaging	HSV1-tk	[18F]FHBG, [18F]FEAU	PET/SPECT or Cerenkov imaging	Monitoring gene therapy, cell trafficking
Photoacoustic Imaging	Tyrosinase (TYR)	None (produces eumelanin)	Ultrasound detection	Deep tissue molecular imaging
RNA In Situ Hybridization	Endogenous genes	Intronic RNAscope probes	Fluorescence microscopy	Cell-type specific nuclear identification

Advanced Integrated Methodologies

Multimodal Optical Pooled CRISPR Screening

Advanced screening methodologies like CRISPRmap combine in situ CRISPR guide-identifying barcode readout with multiplexed immunofluorescence and RNA detection [109]. This approach enables correlation of complex cellular phenotypes—including morphology, protein localization, and cell-cell interactions—with specific genetic perturbations in a spatially resolved manner [109]. The barcode detection system employs combinatorial hybridization of DNA oligos with rolling circle amplification (RCA) and cyclical hybridization readout, achieving high detection efficiency (98% of amplicons coding for allowed barcodes in validation studies) [109].

This methodology is particularly valuable for assessing variants of unknown significance (VUS) in clinically relevant genes. For example, applying CRISPRmap to DNA damage response genes with different DNA-damaging agents (ionizing radiation, camptothecin, olaparib, cisplatin, etoposide) enables variant-specific phenotypic characterization that can prioritize therapeutic strategies [109].

Intronic Probes for Cell-Type Specific Nuclear Identification

Intronic RNA probes address a fundamental challenge in many research areas: unequivocal identification of nuclei belonging to specific cell types. In cardiac regeneration studies, Tnnt2 intronic RNAscope probes specifically label cardiomyocyte nuclei with high accuracy, overcoming limitations of antibody-based approaches that show only 43% sensitivity and 89% specificity [108]. These probes detect intronic RNAs within nuclei, enabling precise identification even during cell division when nuclear envelope proteins are dispersed [108].

The experimental workflow involves:

• Probe Design: Designing oligonucleotide probes complementary to intronic sequences of target genes (e.g., Tnnt2, Myl2, Myl4)
• Tissue Preparation: Fixing tissues in 4% PFA, sucrose saturation, and cryosectioning
• Hybridization: Applying intronic probes with appropriate buffers and washing conditions
• Signal Amplification and Detection: Using RNAscope's proprietary amplification system for single-molecule visualization [108]

This approach enables reliable investigation of DNA synthesis and mitotic activity in specific cell types after injury or in development [108].

Figure 2: Implementation Workflow for Genetic Reporter Systems

The Scientist's Toolkit: Essential Research Reagents

Table 3: Essential Research Reagents for Contrast Mechanism Studies

Reagent Category	Specific Examples	Function/Application	Key Considerations
Extrinsic Dyes	Thioflavin T (ThT), pFTAA, PicoGreen	Detection of protein aggregates, amyloid structures, DNA	Binding specificity, signal-to-background ratio, compatibility with imaging system
Transfection Reagents	Cationic liposomes (Lipofectamine), calcium phosphate	Introduce foreign nucleic acids into eukaryotic cells	Cell type-specific efficiency, toxicity, transient vs stable transfection needs
Viral Vectors	Lentiviruses, retroviruses, vaccinia virus	Stable integration of genetic reporters into host genome	Tropism, packaging capacity, safety considerations, dividing vs non-dividing cells
Genetic Reporters	Fluorescent proteins (EGFP, mCherry), luciferases (NanoLuc), enzymatic reporters (TYR)	Visualize gene expression, protein localization, cell tracking	Brightness, photostability, spectral properties, potential cytotoxicity
Detection Systems	RNAscope probes, immunohistochemistry antibodies, in situ hybridization reagents	Target-specific signal amplification and detection	Sensitivity, specificity, multiplexing capability, background suppression
CRISPR Components	Cas proteins (spCas9, saCas9, asCas12a), guide RNAs, repair templates	Targeted genome editing, gene regulation, screening	Editing efficiency, specificity, PAM requirements, delivery method

The strategic selection of contrast mechanisms represents a fundamental consideration in experimental design for biomedical optics research. Intrinsic contrast mechanisms provide non-invasive approaches for visualizing tissue structure and function but may lack molecular specificity. Extrinsic probes offer enhanced specificity and signal amplification but require introduction of exogenous agents. Genetic reporter systems enable unprecedented capability to monitor dynamic molecular processes in living systems but involve more complex implementation.

Emerging technologies continue to expand possibilities in this domain. Multimodal approaches like CRISPRmap integrate spatial phenotyping with genetic perturbation screening [109]. Advanced probe systems like BETLE reporters enable simultaneous monitoring of multiple editing outcomes [107]. Intronic probing techniques provide unprecedented cellular resolution for identifying specific cell types and their activities [108]. As these technologies mature, they will further empower researchers to visualize and quantify biological processes with increasing precision, ultimately accelerating both basic scientific discovery and therapeutic development.

Understanding the fundamental principles, applications, and methodologies of both intrinsic and extrinsic contrast mechanisms provides researchers with the knowledge needed to select optimal approaches for specific research questions, effectively implement these techniques in experimental workflows, and interpret resulting data within the context of biomedical optics research.

Biomedical optics serves as a fundamental tool in biological research, enabling the visualization and quantification of biological processes from the subcellular level to the level of entire living organisms. The core principle of fluorescence microscopy involves the specific excitation of fluorescent molecules, where light is absorbed by a fluorophore and emitted at a longer wavelength [110]. This principle underpins a wide array of imaging techniques, each designed to overcome specific physical limitations, such as the diffraction limit of light or the scattering of photons in biological tissues. The progression from widefield to confocal and super-resolution microscopy represents an evolution in overcoming these barriers, thereby providing researchers with increasingly detailed views of biological systems. In preclinical models, these optical techniques are indispensable for explaining cellular behaviors, protein interactions, and dynamic physiological processes within the complex native environment of a living animal, directly supporting drug development and basic research.

Core Optical Techniques for Cellular and Subcellular Imaging

Widefield and Confocal Microscopy

The most prevalent fluorescence microscopes are epifluorescence widefield microscopes, where excitation and detection of a signal occur through the same objective light path. In this setup, a dichroic mirror acts as a wavelength-specific filter, transmitting the emitted fluorescence to the detector [110]. While this method allows for rapid image acquisition and direct observation, it carries a risk of high background signal and out-of-focus light, which can blur the final image.

Confocal microscopy addresses this key limitation. It employs a laser for excitation and uses a pinhole placed in front of the detector to physically block out-of-focus light. This configuration ensures that only light from the focal plane reaches the detector, thereby improving image quality and enabling optical sectioning of thick specimens [110] [111]. This capability is crucial for generating clear three-dimensional reconstructions of cellular structures. The trade-off, however, is that image acquisition can be slower compared to widefield microscopy, and the procedure is more complex [110]. For immunofluorescence imaging, it is considered good practice to initially verify staining quality using a widefield microscope before proceeding to confocal microscopy for detailed subcellular localization or protein-protein interaction studies [110].

Super-Resolution Imaging: Breaking the Diffraction Limit

To observe finer subcellular structures, super-resolution techniques that surpass the Abbe diffraction limit are required. Among these, Structured Illumination Microscopy (SIM) is widely used for live-cell imaging due to its relatively low photobleaching and phototoxicity [112]. SIM achieves enhanced resolution by applying a known sinusoidal illumination pattern to the sample. The resulting moiré fringes, which contain high-frequency information from the sample, are computationally processed to reconstruct a super-resolution image [112].

Conventional three-dimensional SIM (3D-SIM) doubles the spatial resolution in all three dimensions but suffers from low temporal resolution. It requires sequential, plane-by-plane movement of the sample using a piezo stage, often taking several seconds to capture a single volume, which hinders the observation of rapid biological processes [112]. A recent development, 3D multiplane SIM (3D-MP-SIM), simultaneously detects images from multiple planes and employs a synergistically evolved reconstruction algorithm. This innovation achieves an approximately eightfold increase in volumetric imaging speed, with lateral and axial resolutions of about 120 nm and 300 nm, respectively [112]. This allows for high-speed time-lapse volumetric imaging of dynamic structures like the endoplasmic reticulum at rates of up to 11 volumes per second [112].

Table 1: Comparison of Key Optical Microscopy Techniques for Cellular Imaging

Technique	Lateral Resolution	Axial Resolution	Key Advantage	Primary Limitation	Best Suited For
Widefield	~250 nm	~500 nm	Fast, easy to use, low cost	High background signal from out-of-focus light	Initial screens, live-cell imaging where speed is critical
Confocal	~180 nm	~500 nm	Optical sectioning, reduced background, improved signal-to-noise	Slower than widefield, more complex operation	3D imaging of fixed cells, thick specimens, multi-color imaging
3D-SIM	~120 nm	~300 nm	2x resolution improvement in 3D, lower phototoxicity	Slow volumetric acquisition (seconds)	Detailed live-cell imaging of dynamic subcellular structures
3D-MP-SIM	~120 nm	~300 nm	Fast volumetric acquisition (up to 11 vols/sec)	Complex instrumentation and reconstruction	High-speed 3D dynamics of organelles and rapid interactions

Advanced Optical Measurement Techniques

Beyond imaging, optical methods are used to determine fundamental material properties. In semiconductor research, which often serves as a model for biological system exploration, several techniques are employed:

• Absorption: Measures the light intensity transmitted through a sample to determine properties like a semiconductor's bandgap, as absorption occurs when light has sufficient energy to excite electrons across the energy gap [113].
• Photoluminescence (PL): Involves measuring the light reradiated by a sample after it absorbs light of a fixed wavelength. The intensity of the emitted light at various wavelengths provides information about the material's electronic structure [113].
• Kerr Rotation: Uses the rotation of linearly polarized light upon reflection from a magnetized material to detect electron spin coherence, which is valuable for studying spin dynamics [113].

Intravital Microscopy: Bridging to Live Animal Imaging

Intravital Microscopy (IVM) encompasses diverse optical systems for directly viewing biological structures and individual cells within live animals, enabling the investigation of key biological phenomena in vivo [111]. This approach overcomes the limitations of traditional in vitro or ex vivo analyses, which can only provide static snapshots of cellular states [111].

The high spatial (∼1 μm) and temporal (sub-second) resolution of IVM allows for the visualization and monitoring of single-cell biological processes, a capability not available with other whole-body imaging modalities like MRI, PET, or SPECT, which have resolutions ranging from 10 μm to 2 mm [111]. IVM has been successfully applied in various fields, including immunology, oncology, and vascular biology, to observe cell trafficking and dynamic behaviors in a native context [111].

Confocal and Multi-Photon Intravital Microscopy

Confocal microscopy setups have been adapted for IVM. However, due to light scattering in tissues, its penetration depth is limited to about 100 μm, and the use of short excitation wavelengths can increase phototoxicity [111].

Multi-photon microscopy (typically two-photon) is particularly advantageous for deep-tissue imaging. Its fundamental mechanism involves the simultaneous absorption of two long-wavelength photons at the laser-focused site to induce fluorescence. Because the probability of two-photon absorption is significant only at the focus, out-of-focus signal is inherently rejected without needing a pinhole [111]. The use of long-wavelength light minimizes scattering and absorption, allowing a penetration depth of up to 300 μm and causing negligible photodamage [111]. Additionally, two-photon microscopy can leverage second-harmonic generation (SHG) to visualize non-centrosymmetric structures like collagen without the need for staining [111].

Table 2: Comparison of In Vivo Imaging Modalities

Method	Spatial Resolution (Preclinical)	Temporal Resolution	Penetration Depth	Imaging Agent	Primary Advantage	Primary Disadvantage
IVM (Confocal)	~1 μm	Sub-seconds - Seconds	< 100 μm	Fluorochromes	Microscopic resolution, live-cell tracking	Limited penetration depth, small field of view
IVM (Two-Photon)	~1 μm	Sub-seconds - Seconds	< 300 μm	Fluorochromes	Deep tissue penetration, low phototoxicity	Limited penetration depth, small field of view
CT	50-200 μm	Minutes	No limit	Iodinated molecules	High spatial resolution, fast cross-sectional images	Poor soft tissue contrast, radiation exposure
MRI	10-100 μm	Minutes - Hours	No limit	Paramagnetic chelates	High soft tissue contrast, anatomical detail	Low sensitivity, long acquisition times
PET	1-2 mm	Seconds - Minutes	No limit	Radioactive compounds	High sensitivity, versatile tracer use	Limited spatial resolution, radiation, high cost

Experimental Protocols and Methodologies

Protocol for High-Speed Live-Cell 3D Super-Resolution Imaging

The following methodology outlines the procedure for conducting 3D-MP-SIM imaging, as described in the recent literature [112].

• Sample Preparation and Staining: Culture cells expressing the protein of interest (e.g., endoplasmic reticulum markers) on appropriate imaging dishes. For immunofluorescence, stain cells with antibodies directly conjugated to a fluorochrome or use fluorochrome-conjugated secondary antibodies. Ensure fluorophores have narrow spectral profiles to minimize channel bleed-through in multi-color experiments [110].
• Microscope Setup and Synchronization: Configure the 3D-MP-SIM microscope, which includes a spatial light modulator (SLM) for pattern generation, an image-splitting prism (ISP) in the detection path to separate fluorescence signals, and two cameras to simultaneously capture eight distinct focal planes. A critical step is to convert the polarization of the three input beams to s-polarization using a high-speed liquid crystal variable retarder (HS-LCVR) to enhance the modulation contrast of the excitation field. Synchronize the SLM pattern generation, camera exposure, laser switching, HS-LCVR operation, and piezo stage movement [112].
• Data Acquisition: For each volume, capture a total of 30 exposures. This comprises five lateral phase shifts, three pattern orientations, and two axial phase shifts (achieved via an optical delay line with a piezo-controlled mirror). Each exposure is typically 10 milliseconds. This simultaneous capture of multiple planes replaces the need for sequential Z-stacking used in conventional 3D-SIM [112].
• Image Reconstruction: Process the raw data using a specialized reconstruction pipeline.
  • Spectrum Separation: First, separate the frequency components (orders 0, ±1, ±2) using the lateral phase shifts. Then, further separate the upper and lower parts of the orders ±1 using the axial phase shift.
  • Parameter Estimation: Estimate the precise illumination pattern parameters for each orientation and phase.
  • Spectrum Shifting and Apodization: Reposition the seven separated components to their original locations in the frequency domain using a 3D wave vector, and apply apodization to suppress noise outside the OTF support.
  • Wiener Filtering and Inverse FFT: Apply a Wiener filter to the reassembled spectrum and perform an inverse Fast Fourier Transform to generate the final super-resolved 3D image [112].

Protocol for Intravital Microscopy of Tumor Microenvironment

This protocol describes the application of real-time IVM to study cellular dynamics in tumors [111].

• Animal Model and Window Preparation: Use genetically engineered reporter mice (e.g., Cx3cr1gfp/+ knock-in mice) to track specific cell types, such as monocytes. Implant a tumor of interest. For longitudinal imaging, surgically implant an abdominal imaging window to allow stable, repeated access to the tumor tissue.
• Vascular Labeling: Intravenously inject a fluorescent dye, such as TRITC-dextran, to make the tumor vasculature visible.
• Microscopy and Image Acquisition: Anesthetize the animal and position it under the objective of a two-photon microscope equipped with video-rate resonant scanning for high temporal resolution. Maintain the animal's physiological conditions (e.g., temperature, breathing) throughout imaging. Focus the laser on the tumor tissue and collect the emitted fluorescence and SHG signals to visualize cells, blood vessels, and collagen structures.
• Data Analysis: Track the motility and behavior of fluorescently labeled cells (e.g., monocyte infiltration) over time using specialized analysis software to calculate parameters like velocity, migration paths, and interaction frequencies with vasculature.

The Scientist's Toolkit: Essential Research Reagents and Materials

Table 3: Key Research Reagent Solutions for Optical Imaging

Reagent / Material	Function	Example Application
Fluorochrome-conjugated Antibodies	Specifically bind to and label target proteins for detection.	Immunofluorescence staining of cellular structures like LAMP1 [110].
Genetically Encoded Fluorescent Proteins (e.g., GFP)	Enable tracking of specific cell types or protein localization in live cells and animals.	Tracking motility of monocytes in Cx3cr1gfp/+ knock-in mice [111].
Fluorescent Dextran	Serves as a intravascular contrast agent to visualize blood vessels.	Visualizing tumor vasculature after intravenous injection [111].
Image-Splitting Prism (ISP)	Optically separates fluorescence emissions to simultaneously image multiple focal planes.	Enabling simultaneous multiplane detection in 3D-MP-SIM [112].
High-Speed Liquid Crystal Variable Retarder (HS-LCVR)	Rapidly modulates the polarization state of excitation light.	Optimizing polarization for high-contrast structured illumination in 3D-MP-SIM [112].
Spatial Light Modulator (SLM)	Generates precise, programmable illumination patterns on the sample.	Creating sinusoidal patterns for structured illumination microscopy [112].

Visualizing Workflows and Optical Pathways

3D-MP-SIM Experimental Workflow

Core Principles of Fluorescence Microscopy

Light Paths in Widefield vs. Confocal Microscopy

Biomedical optical imaging technologies have secured a pivotal role in clinical diagnosis and basic research due to their superior spatial resolution, rich imaging contrasts, and non-ionizing properties. These technologies fundamentally rely on the interaction of light with biological tissues, where incident photons undergo modifications in amplitude/intensity, phase, polarization states, and wavelength through scattering, absorption, tissue birefringence, fluorescence, and nonlinear effects. These light-tissue interactions provide specific contrasts for imaging both structure and function of biological tissues, forming the foundational physics upon which all applied technologies are built [18].

The clinical translation of these optical principles has progressed significantly, particularly in three specialized domains: surgical oncology for breast cancer, functional brain monitoring, and image-guided surgery. This transition from laboratory principles to clinical applications represents a paradigm shift in medical imaging, enabling real-time, high-resolution tissue characterization without ionizing radiation or destructive processing. The convergence of optical technologies with artificial intelligence has further accelerated this translation, enhancing interpretive power and diagnostic accuracy across multiple medical specialties [18] [114].

Breast Cancer Imaging: From Margin Assessment to Molecular Characterization

Technical Landscape of Optical Breast Imaging

Breast cancer surgery faces significant challenges in achieving complete tumor resection, with current reoperation rates reaching 30% due to inadequate margins [115]. Optical imaging technologies offer solutions through label-free, real-time microscopic assessment of tumor margins and microenvironment. The table below summarizes quantitative performance data for emerging optical breast imaging technologies.

Table 1: Performance Metrics of Optical Breast Imaging Technologies

Imaging Technology	Key Measured Parameters	Reported Performance/Outcome	Clinical Translation Stage
Multi-parametric OCE	Multiple elasticity contrasts	Improved visualization of breast cancer margins	Intraoperative assessment [116]
PA/US Fusion Imaging	Optical absorption + anatomical features	Improved diagnostic specificity while maintaining high sensitivity	Multicenter clinical trials (PIONEER) [114]
Digital Holographic Imaging + VGG19	3D tissue information with attention mechanisms	More accurate and reliable interpretation of breast tissue features	Technical development phase [117]
Spatial Offset Raman Spectroscopy (SORS)	Subsurface biochemical composition	Detection of tumor margins at depth	Phantom validation stage [118]

Detailed Experimental Protocol: Multi-Parametric Optical Coherence Elastography (OCE)

Purpose: To overcome imaging artifacts in conventional OCE for intraoperative tumor margin assessment through multiple contrast mechanisms [116].

Materials and Equipment:

• Broadband light source: Typically centered at 1300nm for optimal tissue penetration
• Spectrometer: High-speed line-scan camera for spectral domain detection
• Sample arm optics: Galvanometer scanners for beam steering, objective lens
• Mechanical loading system: Controlled air-puff, compression, or acoustic radiation force excitation
• Phantom validation substrates: Tissue-mimicking materials with calibrated mechanical properties [116]

Procedure:

• System Calibration:
  • Align interferometer arms for optimal fringe contrast
  • Calibrate mechanical excitation parameters (force magnitude, duration)
  • Validate spatial resolution with resolution target

• Data Acquisition:

  • Acquire structural OCT data (B-scans) of breast tissue specimen
  • Apply controlled mechanical excitation to induce tissue deformation
  • Capture subsequent OCT images at multiple time points
  • Repeat process across entire specimen surface in raster pattern

• Multi-Parametric Parameter Extraction:

  • Elasticity modulus: Calculate from stress-strain relationship
  • Shear wave speed: Track propagation of mechanically induced waves
  • Strain rate: Measure temporal evolution of tissue deformation
  • Micro-viscoelastic parameters: Derive from frequency-dependent response

• Image Reconstruction & Co-Registration:

  • Reconstruct parametric maps for each mechanical contrast
  • Apply image fusion algorithms to combine contrast mechanisms
  • Register multi-parametric OCE data with histological sections

• Validation:

  • Compare with gold-standard histopathology (H&E staining)
  • Calculate sensitivity/specificity for tumor detection
  • Assess inter-operator reproducibility [116]

Analytical Methods:

• Machine learning classification: Train random forest or CNN classifiers on multi-parametric features
• Quantitative margin assessment: Compute distance from tumor boundary to resection margin
• Statistical analysis: Compare mechanical parameters between tumor and normal tissue using Mann-Whitney U tests

Research Reagent Solutions for Breast Cancer Imaging

Table 2: Essential Research Materials for Optical Breast Imaging Studies

Reagent/Material	Function/Application	Specific Examples
Tissue-Mimicking Phantoms	System validation and calibration	Poly(dimethylsiloxane) polymer (PDMS), Nylon layers for SORS [118]
Exogenous Contrast Agents	Enhance photoacoustic contrast	Indocyanine green (ICG) for PAT [114]
Molecular Probes	Target-specific tumor imaging	Antibody-fluorophore conjugates for fluorescence-guided surgery [119]
Histology Validation Reagents	Gold-standard correlation	Hematoxylin and Eosin (H&E) for tissue structure [115]

Brain Monitoring: From Benchtop to Real-World Applications

Technical Fundamentals of Neurophotonics

Non-invasive optical brain monitoring techniques leverage the differential absorption spectra of oxygenated and deoxygenated hemoglobin in the near-infrared (NIR) window (650-850nm), known as the "therapeutic and diagnostic window" where light penetration reaches several centimeters due to low absorption [120]. Three major techniques dominate this field:

• Functional Near-Infrared Spectroscopy (fNIRS): Measures hemodynamic responses through photon migration in diffusive media [120]
• Diffuse Correlation Spectroscopy (DCS): Quantifies blood flow using Doppler shifts from moving red blood cells [120]
• Fast Optical Signal (FOS): Detects neuronal activity directly through light scattering changes from ion fluxes [120]

The translation of these techniques from controlled laboratories to real-world environments represents a frontier in neurophotonics, enabled by miniaturization, wearable technology, and advanced noise-rejection algorithms.

Experimental Protocol: Mobile fNIRS for Real-World Brain Monitoring

Purpose: To measure cerebrovascular activity linked to brain function during naturalistic behaviors and environments [121].

Materials and Equipment:

• Wearable fNIRS system: Compact, battery-operated with multiple source-detector pairs (e.g., NIRSense Aerie)
• Optodes: Light-emitting diodes (LEDs) and photodetectors arranged in standardized montages
• Headgear: Flexible cap ensuring optode-scalp contact with minimal motion artifacts
• Auxiliary sensors: Integrated accelerometers, gyroscopes for motion tracking
• Data acquisition unit: Wireless transmission capability for unrestricted movement

Procedure:

• System Configuration:
  • Select optode placement based on international 10-20 system
  • Configure source-detector distances (typically 3cm for cortical penetration)
  • Set sampling rate (typically 10-50Hz) based on expected hemodynamic response

• Pre-Data Collection Quality Assessment:

  • Measure signal-to-noise ratio for each channel
  • Verify scalp coupling through visual inspection of raw intensity
  • Check for ambient light contamination

• Data Acquisition Protocol:

  • Record baseline rest period (5 minutes with eyes open)
  • Implement task protocol with event markers synchronized to fNIRS data
  • Include motion paradigms for artifact characterization
  • Monitor systemic physiology (heart rate, respiration) when possible

• Post-Processing Pipeline:

  • Convert raw light intensity to optical density
  • Apply motion artifact correction (e.g., wavelet-based, PCA)
  • Bandpass filter (0.01-0.5Hz) to isolate hemodynamic signals
  • Convert to hemoglobin concentration changes using Modified Beer-Lambert Law
  • Extract block averages or trial-based responses [121]

Analytical Methods:

• General Linear Model (GLM): Statistical parametric mapping of hemodynamic responses
• Functional connectivity: Compute coherence or correlation between regions
• Inter-brain synchrony: Hyperscanning analysis during social interactions
• Machine learning decoding: Classify cognitive states from multivariate patterns

Quantitative Performance in Brain Monitoring Applications

Table 3: Performance Metrics for Optical Brain Monitoring Technologies

Application Domain	Measured Parameters	Key Performance Metrics	Limitations/Challenges
Mental Workload Monitoring	Prefrontal cortex oxygenation	Real-time classification accuracy >80% for workload levels [121]	Extracerebral contamination, motion artifacts
Social Interaction (Hyperscanning)	Inter-brain synchrony	Significant cross-brain correlation during cooperative tasks (r=0.45-0.65) [121]	Variable cap placement, anatomical differences
High-G Environment Monitoring	Cerebrovascular oxygenation	Real-time feedback during G-force exposure [121]	Signal dropout during extreme motion
Infant Development Research	Visual/auditory cortex activation	Detection of stimulus-locked responses in 70-80% of infants [120]	Limited recording duration, participant compliance

Guided Surgery: Optical Technologies for Precision Tumor Resection

Technical Basis of Fluorescence-Guided Surgery

Fluorescence-guided surgery (FGS) represents one of the most significant innovations in surgical oncology, providing real-time intraoperative distinction between tumor and normal tissue. The fundamental optical principles governing FGS include:

• Excitation: Light at specific wavelength excites fluorescent molecules
• Emission: Fluorescent agents emit light at longer wavelengths
• Contrast Mechanisms: Differential accumulation in tumor vs. normal tissue
• Detection: Specialized cameras detect fluorescence signals amidst background [119]

The clinical translation of FGS has been accelerated by the approval of several fluorescent agents and imaging systems, particularly in neurosurgical applications where maximal safe resection is critical for patient outcomes.

Experimental Protocol: Fluorescence-Guided Brain Tumor Surgery

Purpose: To achieve maximal safe resection of brain tumors using fluorescence for real-time tissue discrimination [119].

Materials and Equipment:

• Fluorescent agents: 5-aminolevulinic acid (5-ALA), indocyanine green (ICG), or fluorescein
• Surgical microscope: Integrated fluorescence filters and cameras
• Excitation light sources: Wavelength-specific LEDs or lasers
• Emission filters: Bandpass filters matched to fluorophore emission spectra
• Image processing software: Real-time background subtraction and contrast enhancement

Procedure:

• Preoperative Preparation:
  • Administer fluorescent agent (e.g., 5-ALA 20mg/kg body weight) 3-6 hours before surgery
  • Protect patient from excessive light exposure to prevent phototoxicity
  • Calibrate fluorescence imaging system using reference standards

• Intraoperative Imaging Protocol:

  • Position surgical microscope with appropriate working distance
  • Switch to blue excitation light (375-440nm for 5-ALA)
  • Observe surgical field through appropriate emission filter (620-710nm for 5-ALA)
  • Capture both white light and fluorescence images simultaneously
  • Document fluorescence intensity at tumor margins

• Tumor Resection Guidance:

  • Use fluorescence to identify tumor tissue beyond visible boundaries
  • Resect fluorescent tissue while preserving non-fluorescent structures
  • Periodically reassess resection cavity for residual fluorescence
  • Obtain tissue samples for correlation with histopathology

• Postoperative Analysis:

  • Correlate intraoperative fluorescence with postoperative imaging
  • Validate with histopathological diagnosis of sampled tissues
  • Quantify extent of resection through volumetric analysis [119]

Analytical Methods:

• Fluorescence quantification: Calculate tumor-to-normal ratio (TNR) from intensity values
• Sensitivity/specificity analysis: Compare fluorescence with histopathological gold standard
• Volumetric analysis: Co-register preoperative and postoperative MRI to quantify residual tumor

Research Toolkit for Fluorescence-Guided Surgery

Table 4: Essential Reagents and Materials for FGS Research

Reagent/Material	Function/Application	Considerations for Use
5-Aminolevulinic Acid (5-ALA)	Induces protoporphyrin IX accumulation in tumor cells	Administered 3-6 hours preoperatively; photosensitivity risk [119]
Indocyanine Green (ICG)	Vascular contrast for perfusion assessment	Rapid clearance from circulation; binds plasma proteins [119]
Fluorescein	Blood-brain barrier disruption marker	Non-specific leakage; lower tumor specificity [119]
Monte Carlo Simulation Tools	Modeling light propagation in tissue	GPU-accelerated frameworks (MCX-ExEm) for predicting fluorescence [118]
Tissue-Simulating Phantoms	System validation and standardization	Custom 3D-printed phantoms with well-characterized optical properties [118]

The clinical translation of biomedical optical technologies continues to accelerate, with photoacoustic-ultrasound fusion imaging positioned to become the "fourth major breast imaging modality" alongside mammography, US, and MRI within 5-10 years [114]. In brain monitoring, mobile fNIRS systems are enabling entirely new research paradigms for studying brain function in naturalistic environments [121]. For guided surgery, the integration of molecularly-targeted fluorophores with advanced imaging systems promises unprecedented precision in tumor resection.

The convergence of optical technologies with artificial intelligence represents perhaps the most significant future direction. Deep learning approaches are already demonstrating remarkable capabilities in mitigating fundamental limitations such as photobleaching in photoacoustic imaging [118] and enhancing signal-to-noise in low-light conditions. As these computational methods mature alongside continued innovation in optical hardware, the clinical impact of biomedical optics will expand further, ultimately fulfilling the field's potential to provide non-invasive, real-time, cellular-resolution imaging across the spectrum of medical specialties.

Conclusion

Biomedical optics stands as a pillar of modern medical research and drug development, offering a unique combination of high spatial resolution, biochemical specificity, and non-ionizing safety. The journey from fundamental light-tissue interactions to sophisticated technologies like OCT and PAT underscores the field's capacity to provide both structural and functional insights. While challenges in light scattering and depth penetration persist, ongoing optimization in device design and the strategic integration of optics with other modalities are continuously expanding its capabilities. Future directions point toward greater molecular specificity with novel contrast agents, the miniaturization of devices for endoscopic and point-of-care use, and an increasingly pivotal role in personalized medicine—from accelerating therapeutic discovery to guiding clinical interventions. For researchers and drug developers, mastering these optical principles is no longer optional but essential for driving the next wave of innovation in biomedical science.

References

• 1. Shining a Light on the Future of Biophotonics - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC12245495/]
• 2. Biomedical optics and photonics for advanced clinical ... [https://www.sciencedirect.com/science/article/abs/pii/S0030399224007230]
• 3. Experimental design and numerical investigation of a ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC7005906/]
• 4. The Measurement of Tissue Optical Properties [https://www.biomedicalinstrumentationsystems.com/the-measurement-of-tissue-optical-properties/]
• 5. Optical Characterization of Biological Tissues Based on ... [https://www.mdpi.com/2075-4418/12/11/2846]
• 6. Tutorial on methods for estimation of optical absorption and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11166171/]
• 7. Optical Properties and Reflectance Spectroscopy in ... [https://www.nature.com/research-intelligence/nri-topic-summaries/optical-properties-and-reflectance-spectroscopy-in-biological-tissues-micro-659777]
• 8. Absorption, scattering, and refractive index of blood and its ... [https://www.frontiersin.org/journals/photonics/articles/10.3389/fphot.2025.1636398/full]
• 9. Evaluation of layered tissue scattering properties: a time ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12279310/]
• 10. A Review of Integrating Sphere Techniques for Measuring ... [https://www.sciencedirect.com/science/article/abs/pii/S0956713525007315]
• 11. Project: Optical Properties [https://omlc.org/~prahl/projects/properties.html]
• 12. 基于多角度激发漫反射光信号的浑浊介质光学特性参数识别研究 [https://www.opticsjournal.net/Articles/OJcdcd34905bf5fbdb/FullText]
• 13. A photoacoustic patch for three-dimensional imaging of ... [https://www.nature.com/articles/s41467-022-35455-3]
• 14. Optimal wavelength selection for optical spectroscopy of ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC5820754/]
• 15. Shortwave-infrared meso-patterned imaging enables label ... [https://www.nature.com/articles/s41467-020-19128-7]
• 16. Interpreting hemoglobin and water concentration, oxygen ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC218761/]
• 17. Anthropomorphic breast phantoms with physiological water , lipid , and... [https://www.spiedigitallibrary.org/journals/journal-of-biomedical-optics/volume-19/issue-02/026012/Anthropomorphic-breast-phantoms-with-physiological-water-lipid-and-hemoglobin-content/10.1117/1.JBO.19.2.026012.full]
• 18. Biomedical optical imaging technology and applications [https://pmc.ncbi.nlm.nih.gov/articles/PMC7370594/]
• 19. A review of clinical photoacoustic imaging: Current and future trends [https://pubmed.ncbi.nlm.nih.gov/31871888/]
• 20. Hybrid Method for Solving the Radiative Transport Equation [https://www.mdpi.com/2304-6732/12/5/409]
• 21. Evaluation of a radiative transfer equation and diffusion ... [https://www.spiedigitallibrary.org/journals/journal-of-biomedical-optics/volume-17/issue-12/126010/Evaluation-of-a-radiative-transfer-equation-and-diffusion-approximation-hybrid/10.1117/1.JBO.17.12.126010.full]
• 22. Radiative transport in the delta-P1 approximation for semi- ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3509770/]
• 23. Experimental validation of a high-resolution diffuse optical ... [https://www.spiedigitallibrary.org/journals/journal-of-biomedical-optics/volume-21/issue-01/016009/Experimental-validation-of-a-high-resolution-diffuse-optical-imaging-modality/10.1117/1.JBO.21.1.016009.full]
• 24. A radiative transfer equation-based image-reconstruction ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC5517057/]
• 25. Numerical study on the validity of the diffusion ... [https://pubmed.ncbi.nlm.nih.gov/17206257/]
• 26. Radiative transfer equation modeling by streamline ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC5996876/]
• 27. Near-Infrared-II Fluorescence Imaging of Tumors with ... [https://www.mdpi.com/1424-8220/25/22/7080]
• 28. Editorial: Near-infrared fluorescence probes for biomedical ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10499351/]
• 29. Advancements in broadband near-infrared spectroscopy ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12481167/]
• 30. a machine learning approach for HCV detection in serum ... [https://www.frontiersin.org/journals/medicine/articles/10.3389/fmed.2025.1596476/full]
• 31. Optical sectioning methods in three-dimensional bioimaging [https://www.nature.com/articles/s41377-024-01677-x]
• 32. Near-Infrared (NIR) Spectroscopy Market Size 2025-2029 [https://www.technavio.com/report/near-infrared-spectroscopy-market-industry-analysis]
• 33. Optical Coherence Tomography: Basic Concepts and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC5682075/]
• 34. Optical Coherence Tomography (OCT): Principle and ... - NCBI [https://www.ncbi.nlm.nih.gov/books/NBK554044/]
• 35. Optical Coherence Tomography [https://eyewiki.org/Optical_Coherence_Tomography]
• 36. High-Resolution Imaging of Morphological Changes ... [https://pubmed.ncbi.nlm.nih.gov/40862983/]
• 37. High-Resolution Imaging of Morphological Changes ... [https://www.mdpi.com/2079-6374/15/8/522]
• 38. Optical coherence tomography angiography - PubMed Central [https://pmc.ncbi.nlm.nih.gov/articles/PMC6404988/]
• 39. Advances in optical coherence tomography: Celebrating its ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12456903/]
• 40. Contrast-enhanced optical coherence tomography with ... [https://www.nature.com/articles/srep23337]
• 41. Recent Optical Coherence Tomography (OCT) Innovations ... [https://www.mdpi.com/2306-5354/12/5/441/review_report]
• 42. Advances in Doppler optical coherence tomography and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC7523705/]
• 43. Doppler Optical Coherence Tomography for Otology ... [https://www.mdpi.com/2076-3417/11/12/5711]
• 44. Advances in Optical Coherence Tomography in 2025 [https://www.mdpi.com/journal/diagnostics/special_issues/MR08814H31]
• 45. Point-of-Care Widefield Retinal OCTA Mosaicking at ... [https://opg.optica.org/abstract.cfm?uri=Translational-2025-TW1F.2]
• 46. Fluorescent probes for bioimaging and biosensing [https://www.nature.com/collections/dadaifebad]
• 47. Overview of diffuse optical tomography and its clinical ... [https://www.spiedigitallibrary.org/journals/journal-of-biomedical-optics/volume-21/issue-09/091312/Overview-of-diffuse-optical-tomography-and-its-clinical-applications/10.1117/1.JBO.21.9.091312.full]
• 48. Near-infrared diffuse optical tomography - PubMed - NIH [https://pubmed.ncbi.nlm.nih.gov/14646043/]
• 49. A quantitative comparison of NIRS and fMRI across multiple ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3021967/]
• 50. Developing Drugs for Optical Imaging January 2025 [https://www.fda.gov/regulatory-information/search-fda-guidance-documents/developing-drugs-optical-imaging]
• 51. Handheld Near-Infrared Spectroscopy: State-of-the-Art ... [https://www.mdpi.com/2227-9040/11/5/272]
• 52. SfNIRS Newsletter March 2025 [https://fnirs.org/sfnirs-newsletter-march-2025/]
• 53. Bio-Optics: Design and Applications (BODA) [https://www.optica.org/events/meeting_archives/2025/bio-optics_design_and_application/]
• 54. Tutorial on photoacoustic tomography - PMC - PubMed Central [https://pmc.ncbi.nlm.nih.gov/articles/PMC4834026/]
• 55. A Practical Guide to Photoacoustic Tomography in the Life ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4980387/]
• 56. Dual-modal photoacoustic and ultrasound imaging [https://www.frontiersin.org/journals/photonics/articles/10.3389/fphot.2024.1359784/full]
• 57. Comparing Deep Learning Frameworks for Photoacoustic ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8165448/]
• 58. Photoacoustic imaging platforms for multimodal imaging [https://pmc.ncbi.nlm.nih.gov/articles/PMC4372714/]
• 59. In vivo co-registered hybrid-contrast imaging by successive ... [https://www.sciencedirect.com/science/article/pii/S2213597923000599]
• 60. A Universal Photoacoustic Tomography Foundation Model ... [https://opg.optica.org/abstract.cfm?uri=ECBO-2025-Tu2A.39]
• 61. All-optical in vivo photoacoustic tomography by adaptive ... [https://www.sciencedirect.com/science/article/pii/S221359792500076X]
• 62. High-fidelity deep functional photoacoustic tomography ... [https://www.sciencedirect.com/science/article/pii/S2213597923000034]
• 63. Ophthalmic drug discovery and development using artificial ... [https://www.nature.com/articles/s41746-025-01954-y]
• 64. Advances in multimodal imaging techniques in nanomedicine [https://pubs.rsc.org/en/content/articlehtml/2025/ra/d5ra03255e]
• 65. Application of optogenetics and in vivo imaging approaches ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC9190069/]
• 66. Recent advances in cellular optogenetics for photomedicine [https://www.sciencedirect.com/science/article/abs/pii/S0169409X22003477]
• 67. Optical Molecular Probes, Imaging and Drug Delivery (OMP) [https://www.optica.org/events/meeting_archives/2025/optical_molecular_probes_imaging_and_drug_delivery/]
• 68. Medical Device Packaging: Best Practices and Regulations [https://www.ready-made.com/blog/medical-device-packaging-best-practices-and-regulations]
• 69. Standards & Practices in Medical Device Packaging [https://vantagemedtech.com/medical-device-packaging/]
• 70. Essential Guide to Medical Devices Packaging [https://www.globalvision.co/blog/medical-devices-packaging-best-practices]
• 71. Considerations for Polymers Used in Ocular Drug Delivery [https://pmc.ncbi.nlm.nih.gov/articles/PMC8831705/]
• 72. How Pharmaceutical & Medical High Barrier Packaging ... [https://www.linkedin.com/pulse/how-pharmaceutical-medical-high-barrier-packaging-uf92f/]
• 73. Challenges and new opportunities on barrier performance ... [https://www.sciencedirect.com/science/article/pii/S0079670021000423]
• 74. Microfluidic technologies for wearable and implantable ... [https://pubs.rsc.org/en/content/articlehtml/2025/lc/d5lc00499c]
• 75. Drug Delivery Technologies Impacting 2025 and Beyond [https://www.pharmaadvancement.com/pharma-trends/drug-delivery-technologies-impacting-2025-and-beyond/]
• 76. Detailed study of laser diode array collimation based on a ... [https://opg.optica.org/viewmedia.cfm?html=true&seq=0&uri=oe-33-2-1791]
• 77. Separation of absorption and scattering properties of turbid ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3469994/]
• 78. Research on target enhancement in turbid media based on ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12586856/]
• 79. Determination of optical properties of turbid media ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2917466/]
• 80. Enhanced computational ghost imaging through dynamic ... [https://www.sciencedirect.com/science/article/abs/pii/S0030401825011939]
• 81. Top 5 Emerging Trends in Nanophotonics [https://www.azonano.com/article.aspx?ArticleID=6971]
• 82. Tissue Phantoms to Advance Biomedical Optical Systems - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC9234512/]
• 83. MTF 3: Aberration compounding, CCD contrast transfer ... [https://www.telescope-optics.net/mtf3.htm]
• 84. Current Developments in Lens Design and Optical Engineering ... [https://spie.org/Publications/Proceedings/Volume/PC13131]
• 85. New validation metric for solid mechanics models [https://www.sciencedirect.com/science/article/pii/S0143816624002859]
• 86. Feature Issue of Applied Optics, Biomedical Optics Express ... [https://opg.optica.org/content/feature/announcement/item/oe-cosi2025]
• 87. Research - Biomedical Optics Laboratory - University of Houston [https://bol.egr.uh.edu/research/]
• 88. 4 Challenges for Mechanical Integration of Optical Systems [https://www.simplexitypd.com/blog/4-challenges-and-solutions-for-mechanical-integration-of-optical-systems/]
• 89. Optical System Design and Challenges [https://www.shanghai-optics.com/about-us/resources/technical-articles/optical-system-design-and-challenges/]
• 90. QUEL Imaging and INO Announce Technology Transfer ... [https://www.prnewswire.com/news-releases/quel-imaging-and-ino-announce-technology-transfer-to-advance-biomedical-optics-302618208.html]
• 91. CT, MRI, and PET Scanners: Unravelling the Differences in Modern Medical Imaging [https://openmedscience.com/ct-mri-and-pet-scanners-unravelling-the-differences-in-modern-medical-imaging/]
• 92. What is the Difference Between an X-ray, CT Scan, PET Scan, and MRI? [https://www.fcneurology.net/what-is-the-difference-between-an-x-ray-ct-scan-pet-scan-and-mri/]
• 93. PET/MRI: Where Might It Replace PET/CT? - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC5623147/]
• 94. Comparison of whole-body 18F-FDG PET/CT and PET/MRI for distant metastases in patients with malignant tumors: a meta-analysis | BMC Cancer | Full Text [https://bmccancer.biomedcentral.com/articles/10.1186/s12885-022-10493-8]
• 95. Comparison of MRI, [18F]FDG-PET/CT, and ... [https://pubmed.ncbi.nlm.nih.gov/40644586/]
• 96. Comparative efficacy and workflow efficiency of integrated ... [https://pubmed.ncbi.nlm.nih.gov/41251733/]
• 97. Validation and Visualization of Two-Dimensional Optical ... [https://pubmed.ncbi.nlm.nih.gov/19013531/]
• 98. Validation and visualization of two-dimensional optical ... [https://www.sciencedirect.com/science/article/abs/pii/S1053811908011002]
• 99. Biomedical Optics - an overview [https://www.sciencedirect.com/topics/physics-and-astronomy/biomedical-optics]
• 100. Virtual Hemodynamic Assessment of Coronary Lesions [https://www.mdpi.com/2077-0383/13/8/2243]
• 101. Tissue clearing protocols [https://www.nature.com/collections/aibiheggij]
• 102. Intrinsic Contrast - an overview [https://www.sciencedirect.com/topics/psychology/intrinsic-contrast]
• 103. Extrinsic Amyloid-Binding Dyes for Detection of Individual ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6127805/]
• 104. Photoacoustic imaging using genetically encoded reporters [https://www.spiedigitallibrary.org/journals/journal-of-biomedical-optics/volume-22/issue-7/070901/Photoacoustic-imaging-using-genetically-encoded-reporters-a-review/10.1117/1.JBO.22.7.070901.full]
• 105. Optical imaging of reporter gene expression using a ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3003718/]
• 106. A Comprehensive Introduction to Magnetic Resonance ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC9609087/]
• 107. A Multifunctional and Highly Adaptable Reporter System ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10179647/]
• 108. Intronic RNAscope probes enable precise identification of ... [https://www.nature.com/articles/s42003-025-08012-z]
• 109. Mapping multimodal phenotypes to perturbations in cells ... [https://www.nature.com/articles/s41587-024-02386-x]
• 110. IF imaging: Widefield versus confocal microscopy [https://www.ptglab.com/news/blog/if-imaging-widefield-versus-confocal-microscopy/?srsltid=AfmBOoqoBpwcxGRMUA9Fyw2meAoLOr7PNdMYxZ2K_53Pwryj_XnCU8ch]
• 111. Recent advances in intravital microscopy for investigation ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC7396917/]
• 112. Fast, three-dimensional, live-cell super-resolution imaging ... [https://www.nature.com/articles/s41566-025-01638-9]
• 113. Optical Experiments on Semiconductors [https://physics.byu.edu/research/coltonlab/optical-experiments]
• 114. Research Progress and Clinical Translation of ... [https://www.sciopen.com/article/10.26599/AUDT.2025.250103]
• 115. Label-free optical imaging technologies for rapid translation ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC5747261/]
• 116. Visualization of Breast Cancer Using Multi-Parametric ... [https://opg.optica.org/abstract.cfm?uri=ECBO-2025-S1C.2]
• 117. Advancements in Breast Cancer Detection and Analysis by ... [https://opg.optica.org/abstract.cfm?uri=COSI-2025-JVD1.5]
• 118. Volume 30 Issue S3 | Journal of Biomedical Optics [https://www.spiedigitallibrary.org/journals/journal-of-biomedical-optics/volume-30/issue-S3]
• 119. Optical Principles of Fluorescence-Guided Brain Tumor Surgery [https://pubmed.ncbi.nlm.nih.gov/30085129/]
• 120. Neurophotonics: non-invasive optical techniques for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4370435/]
• 121. Editorial: Advances in mobile optical brain activity monitoring [https://www.frontiersin.org/journals/neuroergonomics/articles/10.3389/fnrgo.2025.1568619/full]